Задача 37112 Дана пирамида SABC, в которой...

ofofofododk

2019-05-16 09:51:07

Дана пирамида SABC, в которой SC=SB=AB=AC=sqrt(19), SA=BC=2sqrt(6)
А) Докажите , что ребро SA перпендикулярно ребру BC.
Б) Найдите расстояние между ребрами BC и SA.

sova

2019-05-16 13:34:58

Пирамида состоит из четырех одинаковых равнобедренных треугольников.
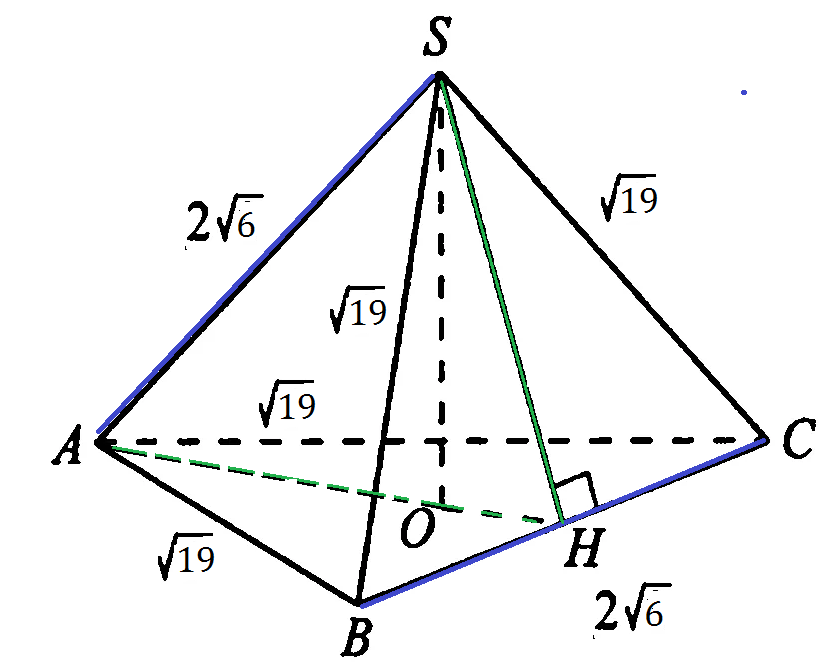
см. рис.
1) SA и BC - скрещивающиеся прямые.

АН - проекция SA на пл. АВС
АН ⊥ ВС, высота равнобедренного треугольника одновременно и медиана

По теореме о трех перпендикулярах, если проекция перпендикулярна ВС, то и наклонная SA перпендикулярна ВС

2)
АН - медиана.
ВН=НС=sqrt(6)

по теореме Пифагора.
SH^2=SB^2-BH^2=(sqrt(19))^2-(sqrt(6))^2=13

SH=AH=sqrt(13)

В треугольнике ASH - перпендикуляр из вершины Н на сторонy SA и есть расстояние между ВС и SA

Перпендикуляр из вершины Н на сторонy SA - высота равнобедренного треугольник АSH.

h^2=AH^2-((1/2)SA)^2=13-6=7

h= [b]sqrt(7)[/b]

О т в е т. sqrt(7)