Задача 37102 Номер 8. В треугольнике ABC угол C равен...

ofofofododk

2019-05-15 22:58:28

Номер 8.
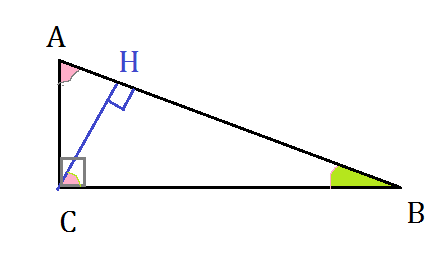
В треугольнике ABC угол C равен 90, CH - высота, CB=sqrt(26), tgA=5. Найдите BH.

sova

2019-05-15 23:18:14

BC=AC*tg ∠ A ⇒ AC=BC/tg ∠ A=sqrt(26)/5

По теореме Пифагора:

АВ^2=AC^2+BC^2=(26/25)+(26)=26^2/25

АВ=26/5


Δ BCН~ ΔBAC ( по двум углам)

BH : BC= BC: AB

BH=BC^2/AB=26/(26/5)=5

О т в е т. [b]5[/b]