Задача 37081 ...
Условие
2^x + 2^(x+2)/(2^x -4) + (4^x+ 7*2^x+20)/(4^x -3*2^(x+2) +32) ≤ 1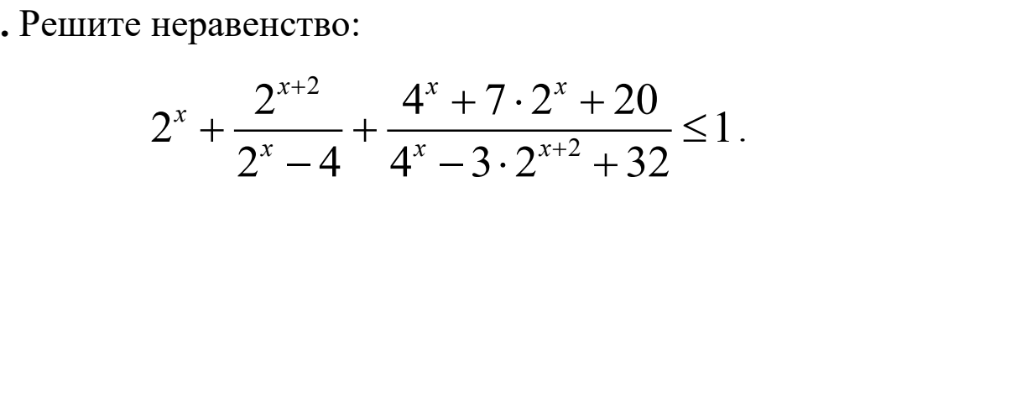
Все решения
t+4t/(t-4) + (t^2+7t+20)/(t^2-12t+32) ≤ 1
t + 4t/(t-4) + (t^2+7t+20)/((t-4)(t-8)) - 1 ≤ 0
[b]([/b]t*(t^2-12t+32)+4t*(t-8)+(t^2+7t+20)-t^2+12t-32 [b])[/b]/((t-4)(t-8)) ≤ 0
(t^3-8t^2+19t-12)/((t-4)(t-8)) ≤ 0
t=1 - корень многочлена t^3-8t^2+19t-12, значит
t^3-8t^2+19t-12=(t-1)(t^2-7t+12)=(t-1)*(t-3)(t-4)
(t-1)*(t-3)(t-4)/((t-4)(t-8)) ≤ 0
(t-1)*(t-3)/(t-8) ≤ 0
t ≠ 4
__-__ [1] __+__ [3] _- _ (4) ____-_____ (8) ___+__
t ≤ 1 или 3 ≤ t < 4 или 4 < t < 8
2^(x) ≤ 1 или 3 ≤2^(x)< 4 или 4 <2^(x)< 8
2^(x) ≤ 2^(0) или 2^(log_(2)3) ≤2^(x)<2^2 или 2^2 <2^(x)< 2^3
О т в е т. [b](- ∞;0] U[ log_(2)3;2) U (2;3)[/b]
