Задача 37043 ...
Условие
lim(x → 2; y → 0) tg(xy)/y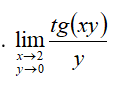
математика ВУЗ
908
Все решения
= lim_(x*y→0) (tg(xy)/(xy))* lim_(x→2; y→0)x=
=1*2= [b]2[/b]
lim(x → 2; y → 0) tg(xy)/y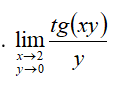
= lim_(x*y→0) (tg(xy)/(xy))* lim_(x→2; y→0)x=
=1*2= [b]2[/b]