Задача 37015 Решите 2-3,а то что-то очень сильно...

vk483915676

2019-05-13 19:25:14

Решите 2-3,а то что-то очень сильно туплю

sova

2019-05-13 19:46:19

2.
ОДЗ:
{x+2>0 ⇒ x>-2
{x+2 ≠ 1 ⇒ x ≠ -1
{7x^2+11x-6>0 ⇒ D=289; x < -2 или x > 3/7

x ∈ (3/7;+ ∞ )

2=log_(x+2)(x+2)^2

Перепишем неравенство в виде:

log_(x+2) (7x^2+11x-6) < log_(x+2)(x+2)^2

При х ∈ (3/7;+ ∞ )

основание логарифмической функции (x+2)>1 , значит логарифмическая функция возрастает и тогда
7x^2+11x-6 < (x+2)^2

6x^2+7x-10 < 0

D=49-4*6*(-10)=289

x=(-7 ± 17)/12

-2 < x < 5/6

С учетом ОДЗ

[b](3/7; 5/6)[/b] - о т в е т.

3.
Дробь равна 0 ⇔ числитель равен 0, а знаменатель отличен от 0

{2sinx+sqrt(3)=0
{2cosx-1≠ 0

{sinx = - sqrt(3)/2
{cosx ≠ 1/2

{х=(-1)^(k)arcsin(-sqrt(3)/2)+πk, k ∈ Z
{x ≠ ± arccos(1/2)+2πn, n ∈ Z

{х=(-1)^(k)(-π/3)+πk, k ∈ Z
{x ≠ ±π/3 +2πn, n ∈ Zππ

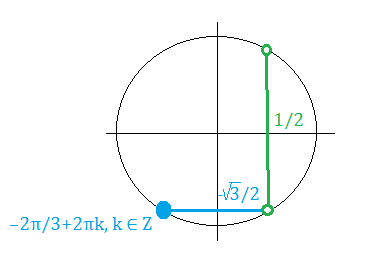
Cм. рис.

О т в е т. [b]-2π/3+2πk, k ∈ Z[/b]