Задача 36999 ...
Условие
1/(log(x-1)x/20 ) ≥ -1
7^(ln(x^(2)-2x)) ≤ (2-x)^(ln7)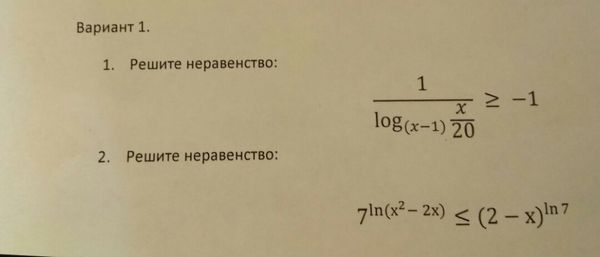
Решение
{x-1>0 ⇒ x > 1
{x-1 ≠ 1 ⇒ x ≠ 2
{x/20>0⇒ x > 0
{log_(x-1)(x/20) ≠ 0 ⇒ x/20≠1⇒ x≠20
ОДЗ: [b]х ∈ (1;2) U (2;20) U (20;+∞ )[/b]
Переносим все слагаемые влево, приводим к общему знаменателю и сравниваем выражение с 0
1+log_(x-1)(x/20))/log_(x-1)(x/20) ≥ 0
1=log_(x-1)(x-1)
Сумму логарифмов в числителе заменим логарифмом произведения
(log_(x-1) (x-1)*x/20)/(log_(x-1)(x/20)) ≥ 0
Применяем формулу перехода к другому основанию
log_(c)b/log_(c)a=log_(a)b
a>0; b>0; c>0 ;c ≠ 1; a ≠ 1
log_(x/20) (x-1)*(x/20) ≥ 0
0=log_(x/20) 1
log_(x/20) (x-1)*(x/20) ≥log_(x/20) 1
Можно рассмотреть два случая:
{(x/20)>1, тогда логарифмическая функция возрастает и
{(x-1)*x/20 ≥ x/20
(2)
{(x/20)< 1, тогда логарифмическая функция убывает и
{(x-1)*x/20 ≤ x/20
или
(1)
{(x/20)-1>0,
{(x-1)*(x/20) - (х/20) ≥ 0
(2)
{(x/20)-1 < 0,
{(x-1)*(x/20) - (х/20)≤ 0
В первой системе оба выражения в первом и во втором неравенстве положительны, во второ1 системе отрицательны. Значит произведение выражений положительно и вместо рассмотрения двух систем можно рассмотреть неравенство, состоящее из произведения
((x/20)-1)*((x-1)*x/20 - (x/20)) ≥ 0
((х-20)/20)* (х/20)* (х-1-1)≥ 0 ( умножаем на 20*20=400)
x*(x-2)*(x-20) ≥ 0
метод интервалов на ОДЗ
(1) _+__ (2) ___-____ (20) ___+____
О т в е т. [b](1;2) U(20;+ ∞) [/b]
ОДЗ:
{x^2-2x>0 ⇒ x(x-2) > 0 ⇒ x < 0 или x > 2
{2-x > 0 ⇒ x < 2
ОДЗ: [b]х ∈ (- ∞; 0)[/b]
Логарифмируем по основанию e
e>1
Логарифмическая функция с основанием e возрастает, поэтому знак неравенства не меняется:
ln 7^(ln(x^2-2x)) ≤ ln(2-x)^(ln7)
Применяем свойство логарифма степени:
log_(a)b^k=klog_(a)b, a>0; a ≠ 1;b>0
ln(x^2-2x)*ln7 ≤ ln7*ln(2-x)
Делим на ln7,
ln7 > 0, знак неравенства не меняется:
ln(x^2-2x) ≤ ln(2-x)
x^2-2x ≤ 2-x
x^2-x-2 ≤ 0
D=1+8=9
корни
-1 и 2
___ (-1) __-__ (2) ___
С учетом ОДЗ получаем ответ
[b](-1;0)[/b]