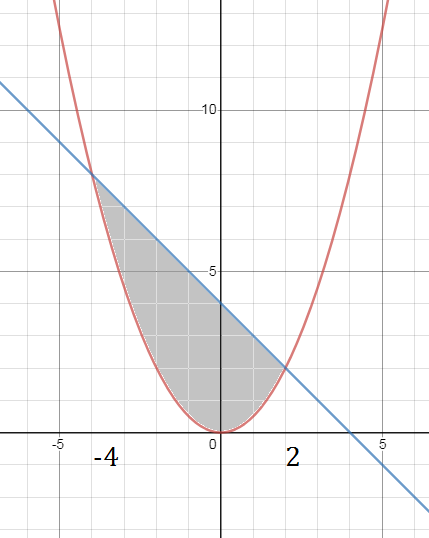
Задача 36993 Решите пожалуйста.Найти объем тел,...
Условие
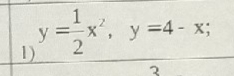
математика ВУЗ
706
Решение
★
=(4x-(x^2/2) -(1/2)*(x^3/3))|^(2)_(-4)=
=4*2-(2^2/2)-(1/6)*2^3- (-16- (16/2)-(1/6)*(-4)^3)= [b]14[/b]