Задача 36991 ...

vk523078937

13 мая 2019 г. в 14:41

1. Вычислите углы треугольника ABC, если ∠ A= ∠ B= ∠ C/2.

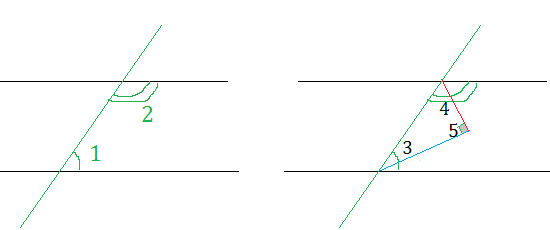
2. Начертите две параллельные прямые и секущую их прямую. Отметьте пару внутренних односторонних углов. Постройте биссектрису каждого из них. Докажите, что эти биссектрисы взаимно перпендикулярны.

sova

13 мая 2019 г. в 16:46

1.
Сумма углов треугольника 180 °.
∠ A+ ∠ B+ ∠ C=180 °
По условию
∠ A= ∠ B= ∠ C/2

∠ C/2 + ∠ C/2 + ∠ C=180 °
2 ∠ С= 180 °
∠ С= 90 °

∠ A= ∠ B= ∠ C/2=90 °/2=45 °

2.
∠ 1+ ∠ 2=180 °

Биссектриса делит угол пополам
∠ 3=(1/2) ∠ 1
∠ 4=(1/2) ∠2


∠ 3+∠ 4=(1/2) ∠ 1+ (1/2) ∠2=90 °

∠ 3+ ∠ 4+ ∠ 5=180 °

90 °+ ∠ 5=180 °

∠ 5= 90 °

Значит биссектрисы пересекаются под углом 90 °, т.е перпендикулярны.