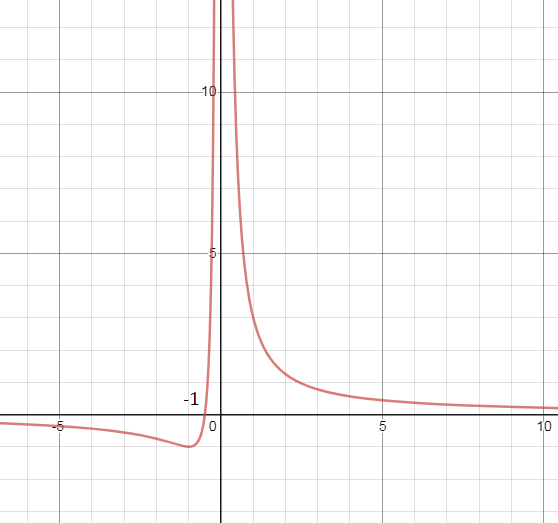
Задача 36971 y=2x+1/x^(2) провести полное...

allk

2019-05-13 06:41:03

y=2x+1/x^(2) провести полное исследование функции и построить график

sova

2019-05-13 17:10:54

★

Область определения (- ∞ ;0)U(0;+ ∞ )

х=0 - не входит в область определения,
является точкой разрыва 2 рода

Прямая x=0 - вертикальная асимптота, так как

lim_(x→0) (2x+1)/x^2=+ ∞

Прямая y=0 - горизонтальная асимптота, так как
lim_(x→ ∞)(2x+1)/x^2= 0


k=lim_(x→ ∞)f(x)/x=lim_(x→ ∞)(2x+1)/x^3= 0

Наклонной асимптоты нет

Находим производную

y`=((2x+1)/x^2)`=((2х+1)`*x^2-(2x+1)*(x^2)`)/x^4=

=(2*x^2-(2x+1)*2x)/x^4=(2x-4x-2)/x^3=-2*(x+1)/x^3

y`=0

x+1=0

x=-1

Знак производной:

__-__ (-1) ___+__ (0) ___-__

y`> 0 на (-1 ; 0); функция возрастает
y` <0 на (- ∞; - 1) и на (0;+ ∞); функция убывает




х=- 1 - точка минимума, производная меняет знак с - на +

[b]y(-1)=-1[/b]

x=0 не является точкой экстремума, так как не входит в Область определениЯ


y``=-2*((x+1)`*x^3-(x+1)*3x^2)/x^6=-2*(x-3x-3)/x^4=(2x+3)/x^4

y``=0

2x+3=0

x=-3/2 - точка перегиба, вторая производная меняет знак.

y``< 0 на (-∞ ; -3/2); функция выпукла вверх
y`` >0 на (- 3/2; 0) и на (0;+ ∞); функция выпукла вниз