Задача 36954 Вычислить объем тела, ограниченного...

qwe6

2019-05-12 17:50:54

Вычислить объем тела, ограниченного поверхностями
z = x^2 + y^2
y = x^2
y=1
z=0

sova

2019-05-12 20:28:38

★

D: -1 ≤ х ≤ 1
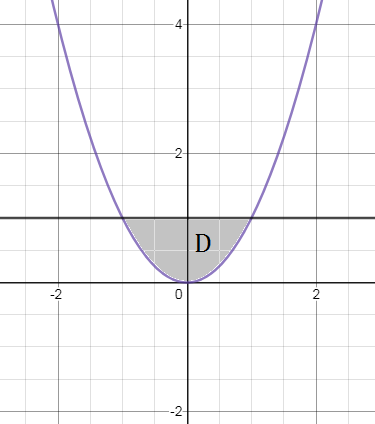
x^2 ≤ y ≤ 1
см. рис.

V= ∫ ∫ _(D) (x^2+y^2)dxdy=

= ∫ ^(1)_(-1)dx ∫ ^(1)_(x^2) (x^2+y^2)dy=

= ∫ ^(1)_(-1) (x^2y+(y^3/3))| ^(1)_(x^2) dx=

= ∫ ^(1)_(-1) (x^2+(1/3)- x^4-(x^6/3)) dx=((x^3/3)+(1/3)x-(x^5/5)-(x^7/21))| ^(1)_(-1) =

=(1/3)+(1/3)-(1/5)-(1/21)-((-1/3)-(1/3)+(1/5)+(1/21)=

= [b]88/105[/b]