Задача 36918 Найти объем тел, образованных вращением...

vk148511207

11 мая 2019 г. в 19:33

Найти объем тел, образованных вращением вокруг оси ох фигуры, ограниченной линиями:
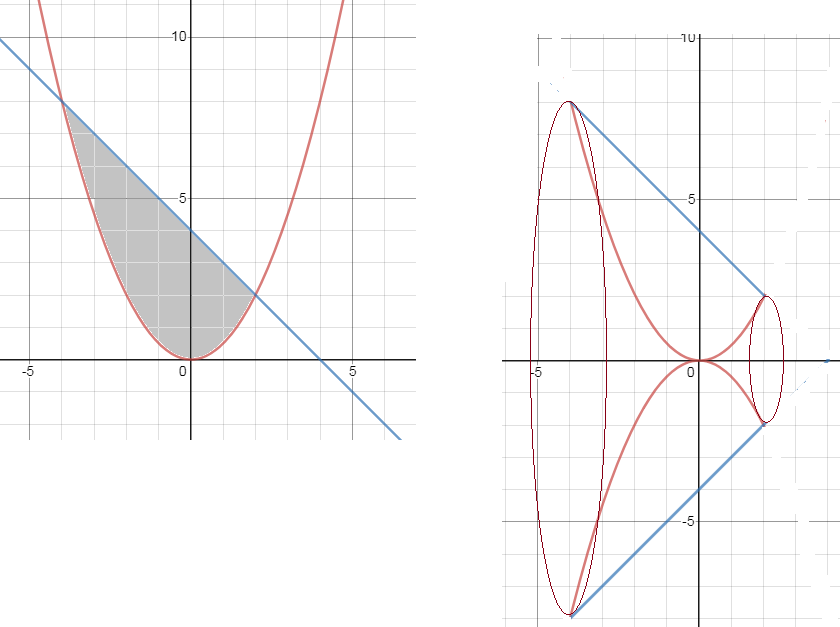
y = 1/2x²
y = 4–x

sova

11 мая 2019 г. в 23:31

★

V_Ох=π ∫ ²_–4 ((4–x)²– ((1/2)x²)² )dx=

=π ∫ ²_–4 (16–8x+x²–(x⁴/4))dx=

=π·( 16x –(8x²/2)+(x³/3)–(x⁵/20))| ²_–4 =

=π·(16·2–4·2²+(1/3)·2³–(2⁵/20) – 16·(–4)+4·(–4)²+(1/3)·(–4)³–(1/20)·(–4)⁵)=

=π·((256/15) +128–(64/3)+(256/5))=