Задача 36909 Найдите все значения а, при каждом из...

vk134969093

2019-05-11 18:08:45

Найдите все значения а, при каждом из которых уравнение
4(ax-x^2) + 1/(ax-x^2) +4 =0
имеет ровно 2 различных корня на промежутке [-1;1).

sova

2019-05-11 19:06:10

★

Дано уравнение, сводящееся к квадратному с помощью замены:

ax-x^2=t

Тогда

4t+(1/t)+4=0

(4t^2+4t+1)/t=0

(2t+1)^2/t=0

2t+1=0
[b]t ≠ 0[/b]

[b]t=-1/2[/b]

ax-x^2=-1/2

Задача сводится к другой задаче.

При каком значении параметра а уравнение

[b]ax-x^2=-1/2[/b]

ax-x^2≠ 0 ⇒ х*(a - x)≠ 0⇒ х≠ 0 и х≠ а

имеет ровно два различных корня на [-1;1)

аx=x^2-(1/2)

a=x - 1/(2x)

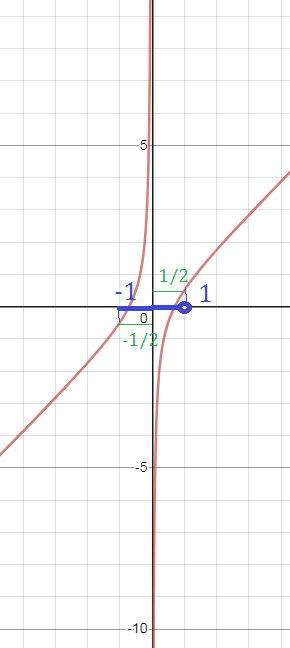
Решаем графически

а=f(x)

Строим прямую y=a
и
Строим график f(x) = x - (1/2x)

Применяем исследование функции с помощью производной.

y`=1-(-1/2x^2)

y`=(2x^2+1)/(2x^2)>0 при любом х.

Функция монотонно возрастает на (- ∞ ;0) и на (0; + ∞)

Строим полосу, ограниченную х=-1 и х=1

При х=-1
y=-1+(1/2)=-1/2
При х=1
y=1-(1/2)=1/2

Т. е [-1;0) U(0;1) → [-1/2;0) U(0;1/2)

Значит при a ∈ [-1/2;0) U (0; 1/2) уравнение имеет два корня.