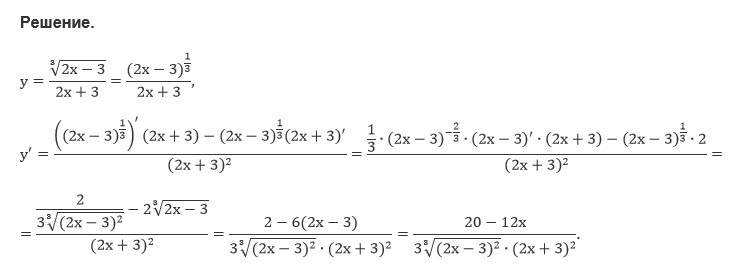Задача 36887 ...

allk

2019-05-11 10:09:23

y=∛(2x-3)/(2x+3) продифферинцировать данные функции

sova

2019-05-11 18:56:38

★

Я думаю, что здесь корень кубический из дроби.

y=∛((2x-3)/(2x+3)).

Для вычисления производной надо знать формулу
(∛x)`=(x^(1/3))`=(1/3)*x^((1/3)-1)=(1/3)x^(-2/3)=1/(3∛x^2)


Для сложной функции

(∛u)`=(u^(1/3))`=u`/(3∛(u^2))


Решение будет выглядеть так:

y`=(1/3)*((2x-3)/(2x+3))^(-2/3)* ((2x-3)/(2x+3))`=

=применяем правило нахождения производной дроби=

=(1/3)* ∛((2х+3)/(2х-3))^2* [b]([/b] ((2x-3)`(2x+3)-(2x-3)*(2x+3)`)/(2x+3)^2 [b])[/b]=

=(1/3)* ∛((2х+3)/(2х-3))^2* [b]([/b] 2*(2x+3)-(2x-3)*2)/(2x+3)^2 [b])[/b]=


=(1/3)* ∛((2х+3)/(2х-3))^2* [b]([/b] (4x+6-4x+6)/(2x+3)^2 [b])[/b]=

=(1/3)* ∛((2х+3)/(2х-3))^2* [b]([/b] (12)/(2x+3)^2 [b])[/b]=

= [b]4/(∛(2x-3)^2*∛(2x+3)^4)[/b]