Задача 36798 log(4)(x-2) + log(1/2)(x-2) = 1/2...
Условие
математика 10-11 класс
3610
Решение
★
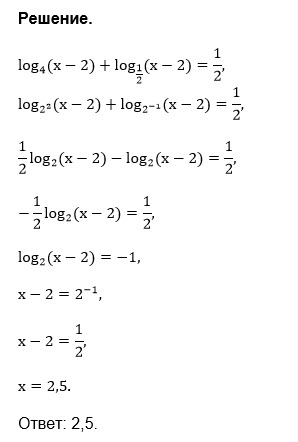
Все решения
x-2 >0 ⇒ х>2
По формуле перехода к новому основанию
log_(4)(x-2)=log_(2)(x-2)/log_(2)4=(log_(2)(x-2))/2= (1/2)*log_(2)(x-4)
log_(1/2)(x-2)=log_(2)(x-2)/(log_(2)1/2)=log_(2)(x-2)/(-1)
Уравнение принимает вид
(1/2) log_(2)(x-2) - log_(2)(x-2)=1/2
(1-(1/2))*log_(2)(x-2)=1/2
log_(2)(x-2)=-1
По определению логарифма
x-2=2^(-1)
x-2=1/2
x=2+(1/2)
x=5/2
5/2 > 2 найденный корень входит в ОДЗ
О т в е т. 5/2