Задача 36715 (4^(x+2))^x * 3 sqrt(32^(x-1)) =64...
Условие
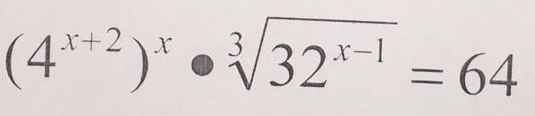
математика 10-11 класс
1798
Все решения
( (4^(x+2))^x=64/∛(32^(x-1)
Упростим обе части уравнения:
((4^(x+2))^x=2^(2x^2+4x)
64/∛(32^(x-1)=2^6/∛(2^(5x-5)=2^(23-5x)/3. Получили обе части уравнения с одинаковым основанием. Решаем уравнение
2^(2x^2+4x)=2^(23-5x)/3.отсюда получаем : 2x^2+4x=(23-5x)/3. или
6x^2+17x-23=0 Так как в уравнении a+b+c=0. то x1=1; x2=-23/6.
Проверка показывает,что найденные значения являются корнями исходного уравнения.
Ответ:x1=1; x2=-23/6.
