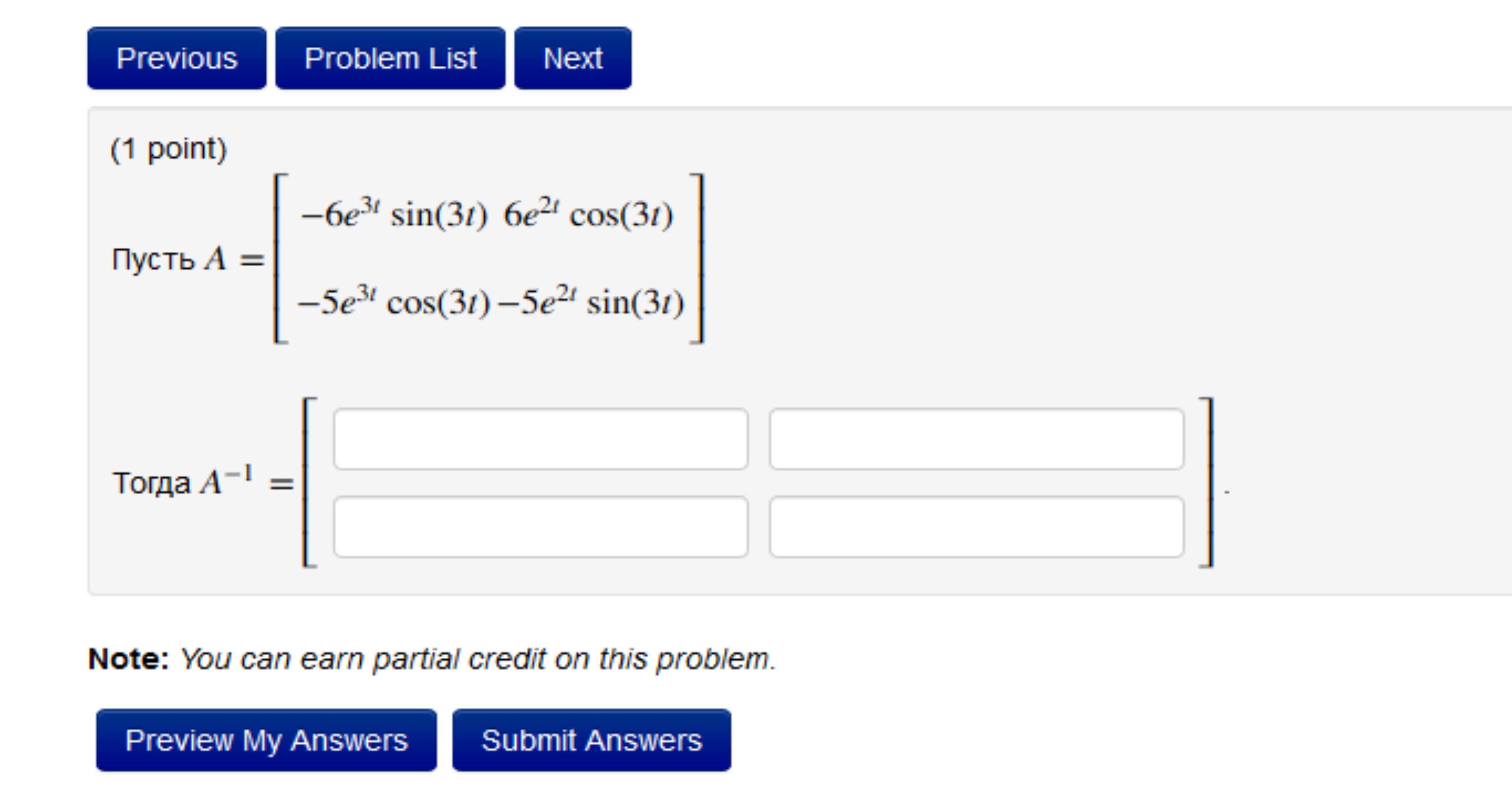
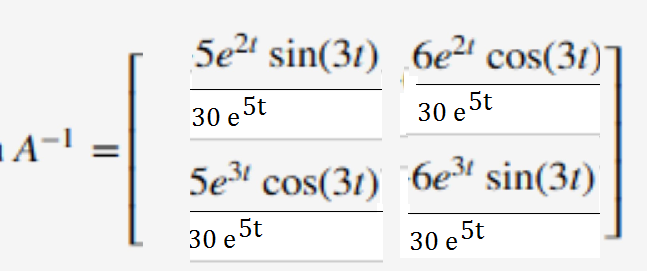Задача 36699 A=[-6e^(3t)sin(3t) 6e^(2t)cos(3t) ...
Условие
-5e^(3t)cos(3t) - 5e^(2t)sin(3t)]
математика
1218
Решение
★
=30e^(5t)*(sin^23t+cos^23t)=30e^(5t)·1=30e^(5t)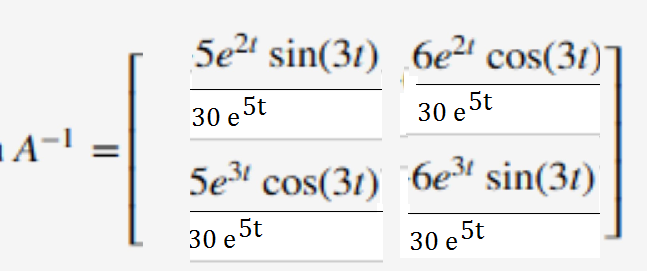
-5e^(3t)cos(3t) - 5e^(2t)sin(3t)]

=30e^(5t)*(sin^23t+cos^23t)=30e^(5t)·1=30e^(5t)