Задача 36678 Основанием прямого параллелепипеда...
Условие

математика 10-11 класс
4373
Решение
★
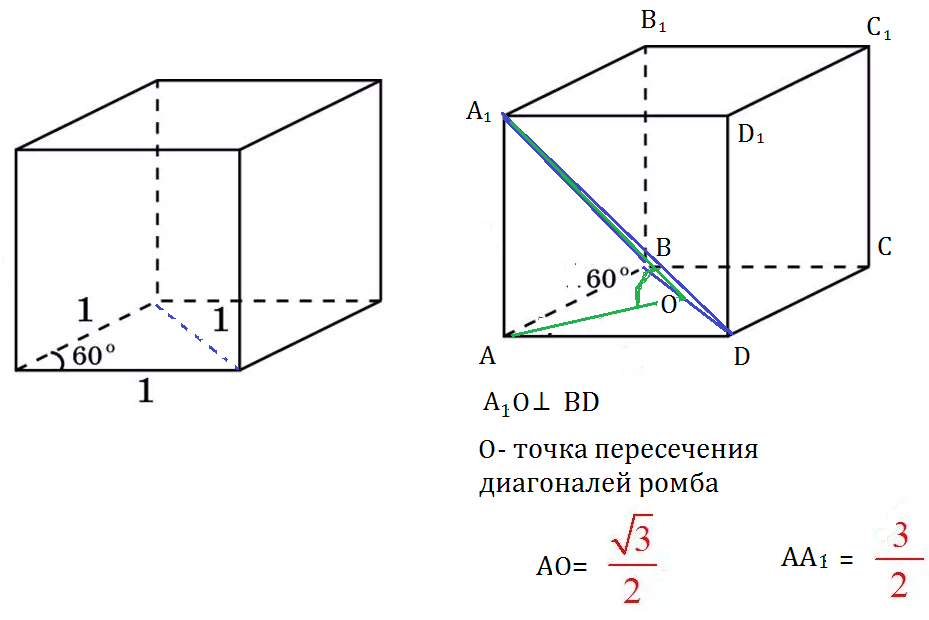
BD=1 , треугольник АВD - равнобедренный с углом 60 градусов при вершине, значит он равносторонний
AO=(1/2)AC
AO^2=AD^2-DO^2=1-(1/2)^2=3/4
AO=sqrt(3)/2
AA_(1) находим из прямоугольного треугольника АА_(1)О
AO=(1/2)AC=sqrt(3)/2
AA_(1)=AO*tg60^(o)=(sqrt(3)/2)*sqrt(3)= [b]3/2[/b]
S_(бок.пов)=P_(осн.)*H
H=AA_(1)
так как призма прямая
Р_(осн)= [b]4[/b]
S_(бп)=4*(3/2)= [b]6[/b]