Задача 36667 задание 25. (3/(2x+1) + log(2)(x+2)/4) /...

vk311264077

2 мая 2019 г. в 15:39

задание 25.
(3/(2x+1) + log₂(x+2)/4) / √–x > 0

sova

2 мая 2019 г. в 16:01

★

ОДЗ:
{–x > 0 ⇒ x < 0
{2x+1 ≠ 0 ⇒ x ≠ –1/2
{(x+2)/4 > 0 ⇒ x > –2

(–2;–1/2) U (–1/2; 0)

На ОДЗ
√–x > 0,
поэтому
осталось решить неравенство:

3/(2x+1) + log₂ (x+2)/4 > 0

3/(2x+1) + log₂ (x+2)– log₂4 > 0

log₂ (x+2) > 2– (3/(2x+1))

log₂ (x+2) > (4x–1)/(2x+1)

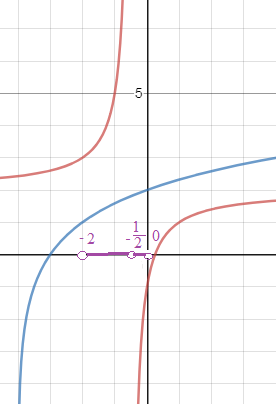
Строим график у=log₂ (x+2)
и
у= (4x–1)/(2x+1)

О т в е т. (–1/2;0)