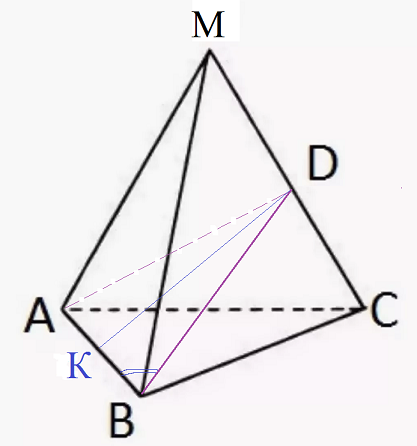
Задача 36626 В правильном тетраэдре МАВС, все ребра...

radostmalchikov

2019-05-01 06:57:47

В правильном тетраэдре МАВС, все ребра которого равны 1 , найдите угол между медианой ВD грани МВС и плоскостью MAB.

sova

2019-05-01 10:29:25

★

Δ MBC- равносторонний
BD- медиана высота и биссектриса
BD=sqrt(3)/2
Проводим AD
Δ MAC- равносторонний
AD=BD=sqrt(3)/2

ΔADB - равнобедренный.
Проводим высоту DK.
BK=KA
BK- проекция BD

Угол между прямой и плоскостью - угол между прямой и ее проекцией на эту плоскость.
Значит, надо найти угол DBK

cos ∠ DBK=BK/BD=(1/2)/sqrt(3)/2=1/sqrt(3)=sqrt(3)/3
[b]∠ DBK= arccos(sqrt(3)/3)[/b] - о т в е т.