Задача 36623 В правильной шестиугольной призме...
Условие
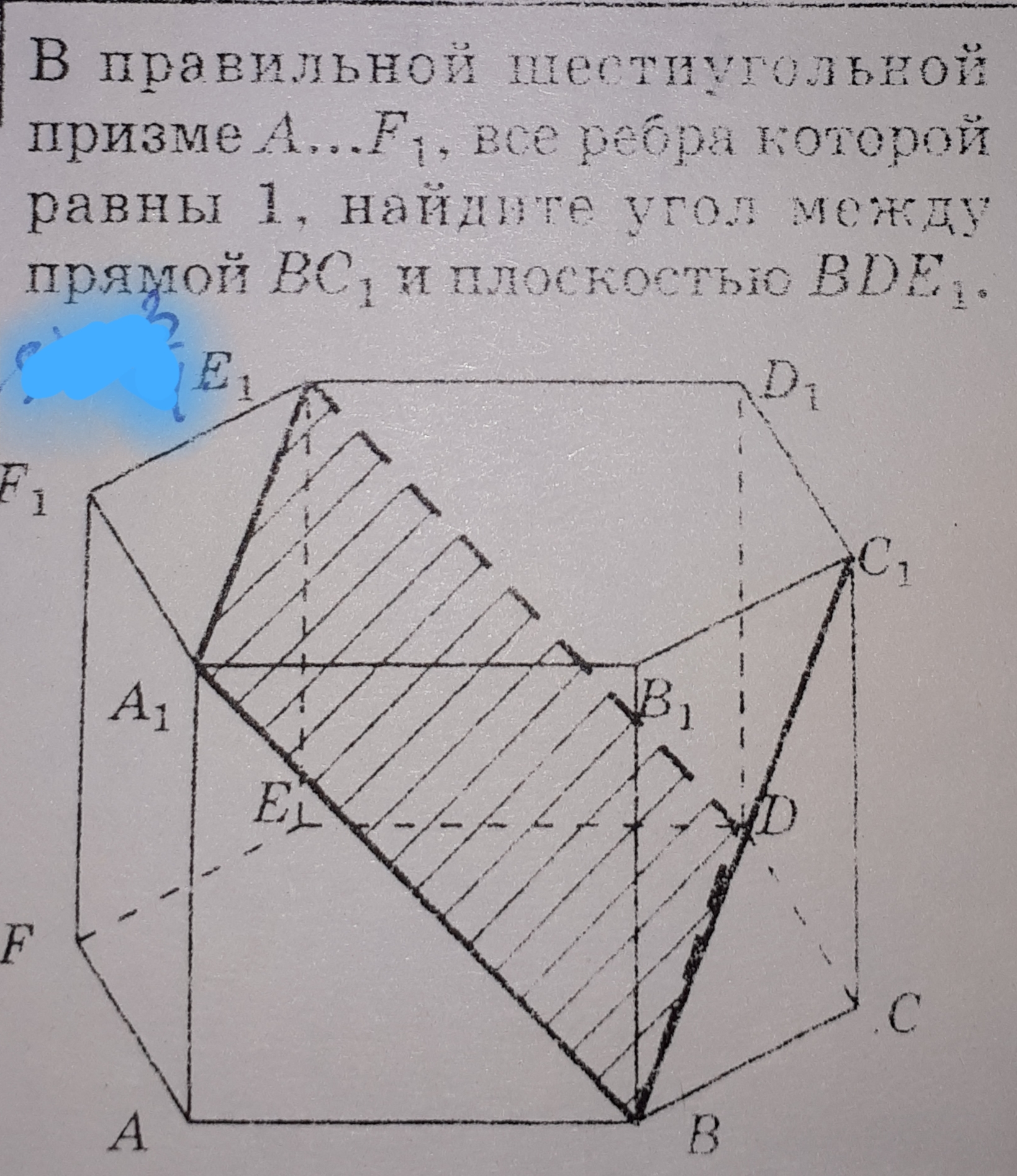
Решение
Cоставляем уравнение плоскости А_(1)Е_(1)BD, проходящей через три точки:
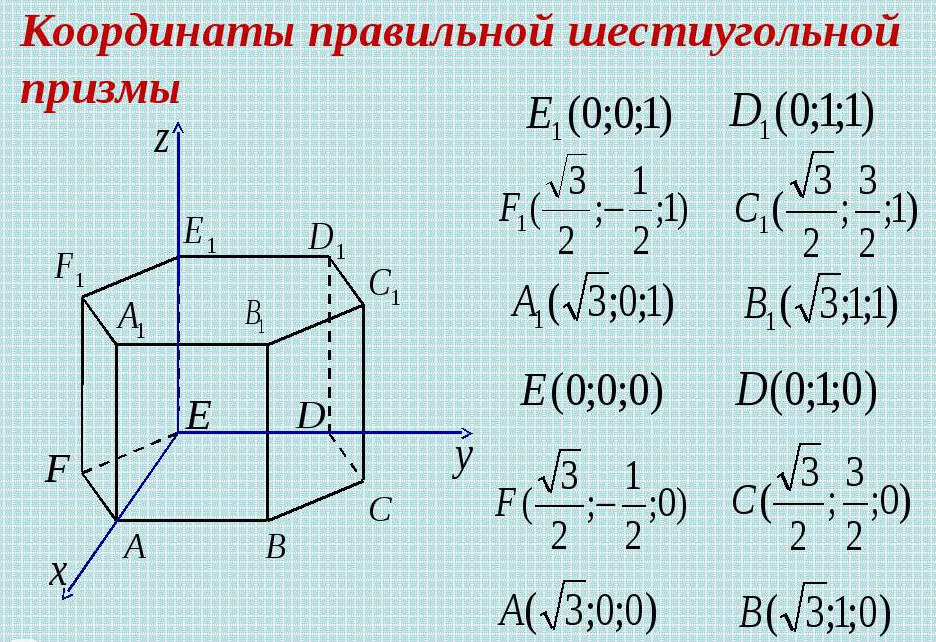
A_(1) (sqrt(3);0;1)
B(sqrt(3);1;0)
D(0;1;0)
Пусть М(х;y;z) - произвольная точка плоскости.
Тогда векторы
vector{DM}=(x;y-1;z)
vector{DA_(1)}=(sqrt(3);-1;1)
vector{A_(1)B}=(0;1;-1)
компланарны.
Определитель третьего порядка, составленный из координат этих векторов равен 0
y+z-1=0
Нормальный вектор плоскости
vector{n}=(0;1;1)
vector{BC_(1)}=((sqrt(3)/2)-sqrt(3);(3/2)-1;1-0)=((-sqrt(3)/2);1/2;1)
Находим скалярное произведение
vector{n}*vector{BC_(1)}=1*(-sqrt(3)/2)+1*(1/2)+1*1=3/2
cos∠(vector{n},vector{BC_(1)})=(3/2)/(sqrt(2)*sqrt(2))= [b]3/4[/b]
Это угол между нормалью и прямой BC_(1)
А угол между прямой и проекцией дополняет данный угол до 90 градусов.
cos(90^(o)- φ)=3/4
sinφ=3/4
О т в е т. arcsin(3/4)
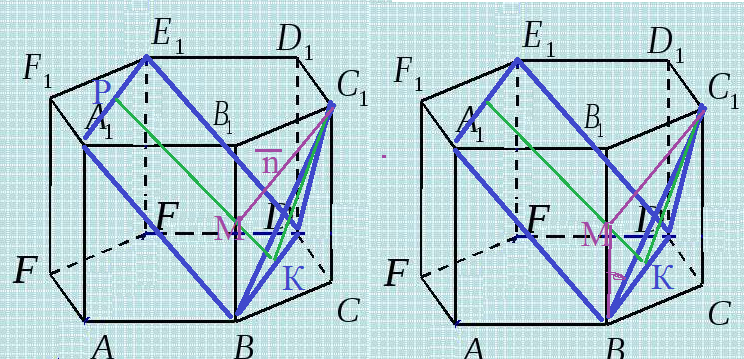
Геометрический способ решения:
(см. рис.2)
Пл. сечения А_(1)Е_(1)BD- прямоугольник ( можно доказать)
(FC⊥BD)
Угол между прямой и плоскостью- угол между прямой и ее проекцией на плоскость. См. рис.
Это угол С_(1)ВМ.
С_(1)M ⊥ PK
sin ∠ С_(1)ВМ=C_(1)M/C_(1)B
C_(1)M=sqrt(2) - диагональ квадрата со стороной 2
PC_(1)=F_(1)C_(1)-F_(1)P=2-(1/2)=3/2
ΔC_(1)BK:
C_(1)K^2=C_(1)B^2-BK^2=(sqrt(2))^2-(sqrt(3)/2)^2=2-(3/4)=5/4
C_(1)K=sqrt(5)/2
Δ PC_(1)K
PK=A_(1)B=sqrt(2)
cos ∠ PC_(1)K=1/sqrt(5) по теореме косинусов из Δ PC_(1)K
sin ∠ PC_(1)K=2/sqrt(5)
C_(1)M*PK=PC_(1)*C_(1)K*sin ∠ PC_(1)K
C_(1)M=3/2sqrt(2)
sin ∠ С_(1)ВМ=C_(1)M/C_(1)B=3/(2*sqrt(2)*sqrt(2))= [b]3/4[/b]
О т в е т. arcsin(3/4)