Задача 36467 Найти площадь прямоугольного...

sova

26 апреля 2019 г. в 21:10

Найти площадь прямоугольного треугольника,вписанного в окружность радиуса 17,если одна из его сторон стягивает дугу 30 °.

Если прямоугольный треугольник вписан в окружность, то прямой угол опирается на диаметр.
c=2R=34
Значит гипотенуза треугольника есть диаметр окружности

Вписанный угол измеряется половиной дуги, на которую он опирается. Значит один угол треугольника 15 °, второй –75 °

a=34·sin15 °
b=34·cos15 °

S Δ ABC= (1/2)·a·b=(1/2)·34·sin15 °·34·cos15 °=289·sin30 °=289/2=144,5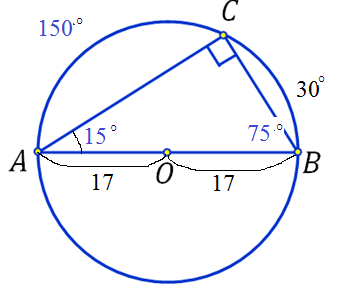

Ответ: 144,5

vk397114329

24 апреля 2020 г. в 18:14

★

Провести диаметр CD
Четырехугольник ADBC–прямоугольник (AB=CD; ∠ C= ∠ D=90·)
∠ COB=30· (как центральный опирающийся на дугу 30·)
S ΔABC=1/2(S четырехугольника ADBC)
S(ADBC)=1/2AB·DC·sin30·=1/2·AB·DC·sin30·=0,25·34·34=289
S ΔABC=0,5·289=144,5
Ответ: 144,5.