Задача 36442 Вариант 7. 1. Вычислить площадь фигуры,...

vk96124622

26 апреля 2019 г. в 12:47

Вариант 7.
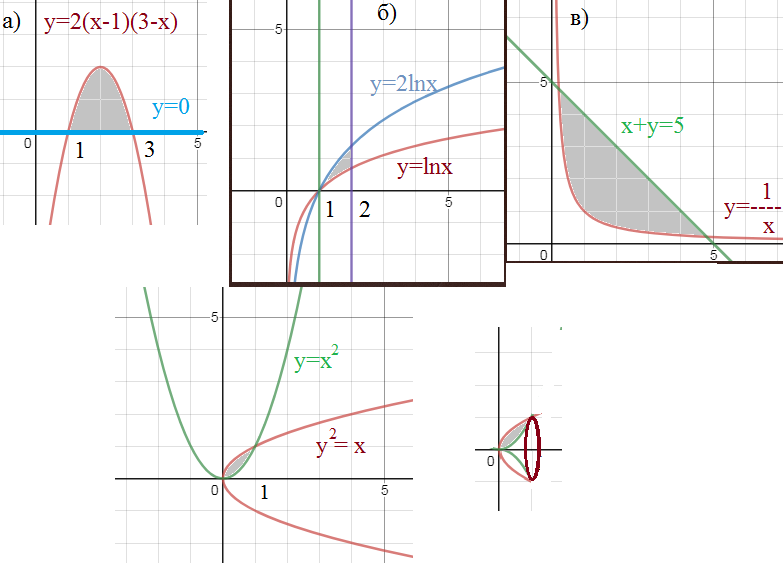
1. Вычислить площадь фигуры, ограниченную линиями:
a) y = 2(x – 1)(3 – x); y = 0.
б) y = ln x; y = 2 ln x; x = 1; x = 2.
в) y = 1/x; x + y = 5.

2. Вычислить объем тела, полученного вращением вокруг оси OX линий
y² = x; y = x².

sova

26 апреля 2019 г. в 20:49

1 a)
S= ∫ ³₁2(x–1)·(3–x)dx=2·∫ ³₁(–x²+4x–3)dx=

=2·((–x³/3)+4·(x²/2)–3x}|³₁=2·(–9)+2·9–3·3 – 2·(–1/3)–2·(–1)²+6·(–1)=


1б)
S= ∫ ²₁(2lnx–lnx)dx= ∫ ²₁lnxdx= интегрируем по частям=

[ u=lnx; du=dx/x; dv=dx; v=x]

=xlnx|²₁ – ∫ ²₁x·dx/x=

=2ln2–1ln1–(x)²₁= 2ln2–1

1в)
Найдем абсциссы точек пересечения:
{y=1/x
{x+y=5

х+(1/х)=5
x²–5x+1=0
D=25–4=21
x₁=(5–√21)/2; х₂=(5+√21)/2


S= ∫ x2x1(5–x–(1/x))dx=

=(5x–(x2/2)–lnx)|x2x1

2.
y²=x⇒ y=√x
f(x)=√x


y=x²⇒ g(x)=x²

По формуле:

V_{вращения Ох}=π ∫ ^b_a (f²(x)–g²(x))dx


V_{вращения Ох}=π ∫ ¹₀x dx – π ∫ ¹₀x⁴ dx=

=π·(x|¹₀ –(x⁵/5)|¹₀)=π·(1–(1/5))= 4π/5