Задача 36435 Решить методом непосредственного...
Условие
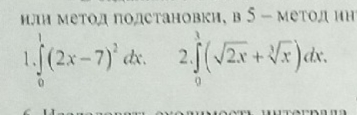
математика ВУЗ
782
Решение
★
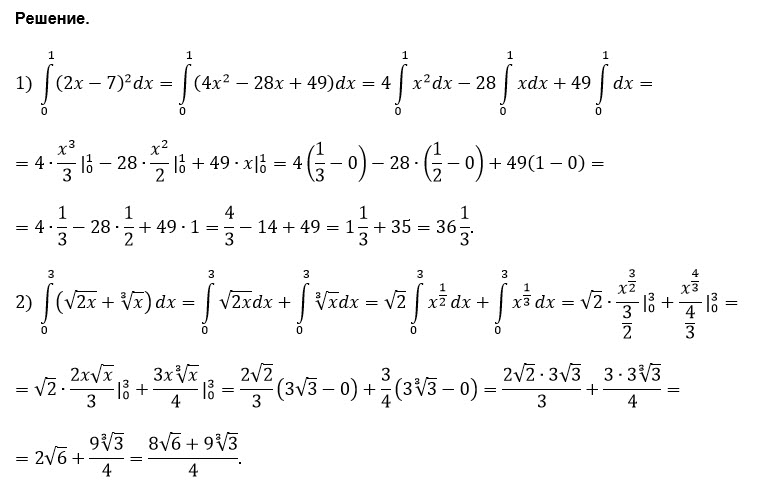
Все решения
∫ u^2du
d(2x-7)=2dx
dx=(1/2)d(2x-7)
=(1/2) ∫ ^(1)_(0)(2x-7)^2d(2x-7)=((1/2)*(2x-7)^3/3)|^(1)_(0)=
=(1/6)*(2*1-7)^3-(1/6)*(2)*0-7)^3=(1/6)(-5)^3-(1/6)*(-7)^3=
=(1/6)*(7^3-5^3)=(1/6)*(7-5)*(7^2+7*5+5^2)=109/3= [b]36 (1/3)
[/b]
2.
Метод замены
x=t^6
sqrt(x)=t^3
∛x=t^2
dx=6t^5dt
Пределы интегрирования:
если x=0, то t=0
если х=3, то t=3^(1/6)
= ∫^(3^(1/6))_(0) (sqrt(2)*t^3+t^2)6t^5dt=
=6sqrt(2) ∫^(3^(1/6))_(0)t^8dt+6 ∫^(3^(1/6))_(0)t^7dt=
=6sqrt(2)*(t^9/9)|^(3^(1/6))_(0)+6*(t^(8)/8)|^(3^(1/6))_(0)=
=(2/3)sqrt(2)*3^(3/2)+(3/4)3^(8/6)=
=(2/3)sqrt(2)*3sqrt(3)+(3/4)*3∛3=
= [b]2sqrt(6)+(9/4)*∛3[/b]