Задача 36429 1. Радиус основания цилиндра 12 см, а...

qwertyfamithds

2019-04-25 21:00:39

1. Радиус основания цилиндра 12 см, а его образующая 8 см. Найти площадь полной поверхности цилиндра, площадь осевого сечения.

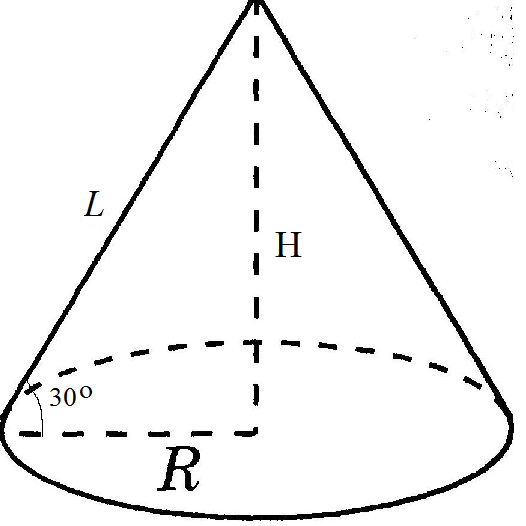
2. Образующая конуса наклонена к плоскости основания под углом 30 градусов, а его высота равна 4 см. Найдите площадь основания.

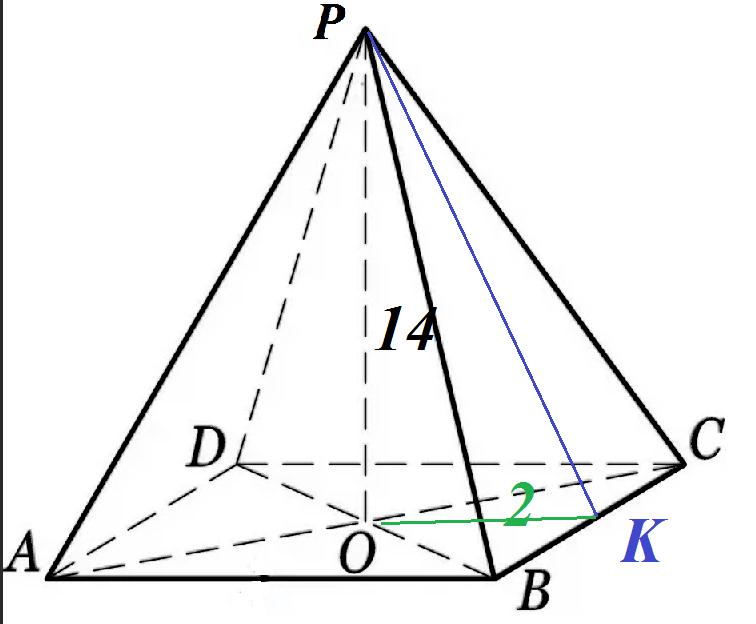
3. В правильной четырехугольной пирамиде сторона основания равна 4 см, а высота 14 см. Найдите площадь основания полной поверхности.

sova

2019-04-25 22:13:41

★

1.
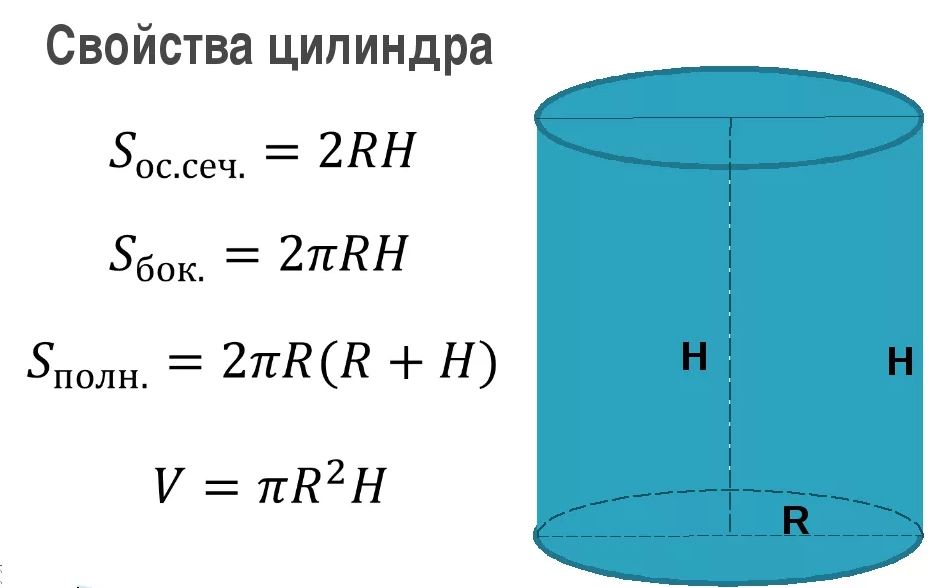
S_(пп)=S_(бп)+2S_(осн)=2πR*H+2*π*R^2=2π*12*8+2*π*12^2=

=(192π+288π)см^2

S_(осев. сеч)=D*H=2R*H=2*12*8=192 см^2

2.
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы
L=2H=8 см
По теореме Пифагора
R^2=L^2-H^2=8^2-4^2=64-16=48
R=4sqrt(3)

S_(осн)=πR^2=48π см^2

3.
Апофема BK=sqrt(14^2+2^2)=sqrt(200)=10sqrt(2)

S_(бп)=P_(осн)*BK/2=4*4*10sqrt(2)/2=80sqrt(2)
S_(осн)=4^2=16

S_(пп)=S_(бп)+S_(осн)=80sqrt(2)+16