Задача 3630 В вершинах равнобедренного треугольника...

slava191

23.09.2015

В вершинах равнобедренного треугольника со сторонами а, 5а, 5а находятся неподвижно три небольших по размерам положительно заряженных шарика, связанных попарно тремя легкими непроводящими нитями. Каждый из шариков, связанных короткой нитью, имеет массу m и заряд q. Третий шарик имеет массу 2m и заряд 5q. Короткую нить пережигают, и шарики начинают двигаться. В момент, когда шарики оказались на одной прямой, скорость шариков массой m оказалась v.

1) Найдите в этот момент скорость шарика массой 5m.

2) Найдите q, считая известными m, v, а.

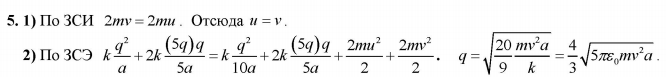
Ответ: В решение