Задача 36230 Подробно!!!...

raffaello

2019-04-22 21:40:53

Подробно!!!

befunny

2019-04-22 22:27:45

Допустим, что левая часть равняется нулю. Значит, числитель равняется нулю. А это утверждение ложно, т.к. любая степень числа- это, возможно, маленькое, но все же положительная величина.
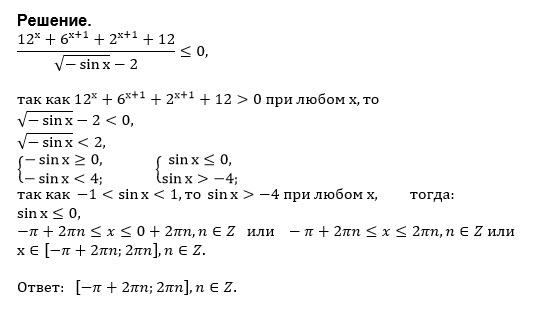
Теперь, когда мы разобрались, что левая часть не равна нулю, подумаем при каких x она может быть меньше нуля. Числитель, как сказано выше, неотрицателен, следовательно, отрицательным должен быть знаменатель.
Во-первых, -sinx ≥ 0(по определению подкоренного выражения);
Во-вторых, синус определяется на интервале от 1 до -1(иначе говоря, 1 ≥ sinx ≥ -1);
Заметим, что синус не может быть больше нуля, т.к. под корнем будет отрицательное выражение. ⇒ наше "о.д.з" для синуса: -1 ≤ sinx ≤ 0. А теперь логика. При любом значении из этой области знаменатель будет отрицателен и решение будет определенно, значит нам подходят все числа из этого промежутка.
Однако, это область допустимых значений для синуса x, а не для самого x.
x=-1 в точке 3π/2 и будет повторяться через каждый оборот круга, т.е. 3π/2+2πk,k ∈ Z;
x=0- частный случай, ответ под это- πn , n ∈ Z;

[b]Ответ: 3π/2+2πk,k ∈ Z ≤ x ≤ πn.[/b]

[r]P.S. Я не уверен в этом ответе, так как он представляет собой бесконечное множество решений. Поэтому, если есть время и нет желания переписывать бред- подожди кого-нибудь ещё. [/r]

[r]P.P.S. В решении не учтена 4-ая четверть. Т.к. это круг, то граница 3π/2- грубая ошибка. Правильный ответ- [π+πn, n ∈ Z; 2πk, k ∈ Z]. [/r]