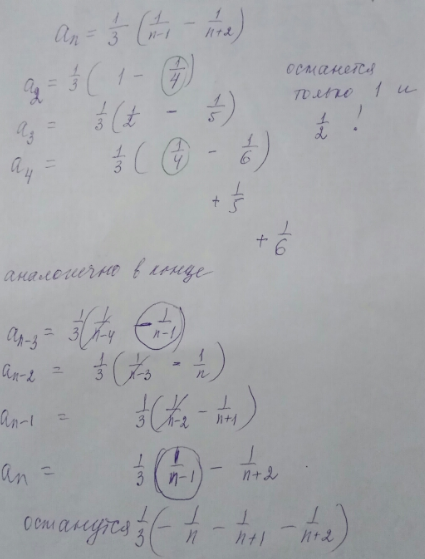Задача 36227 ...
Условие
Решение
Так и скажите преподавателю.
Но метод решения таков
Раскладываем знаменатель на множители
n^2+n-2=(n-1)(n+2)
а дробь на простейшие ( как в интегрировании)
1/(n^2+n-2)= A/(n-1) + B/(n+2)
1=A*(n+2)+B*(n-1)
При n=-2
1=-3B
B=-1/3
При n=1
1=3A
A=1/3
1/(n^2+n-2)= (1/3) * (1/(n-1) - 1/(n+2))
Считаю сумму от двух!
S_(n)=∑^( n )_( [b]2[/b]) (1/3) * [b]([/b]) 1/(n-1) - 1/(n+2) [b])[/b]) =
(1/3) [b]([/b]1-1/4+1/2-1/5+1/4- 1/6 +...
+1/(n-4)-1/(n-1)+1/(n-3)- 1/n+ 1/(n-2) - 1/(n+1)+1/(n-1) - 1/(n+2) [b])[/b]=
=(1/3)* [b]([/b]1 +(1/2)- 1/n -1/(n+1) - 1/(n+2) [b])[/b]
Удобнее записать сумму "лесенкой" : так хорошо просматривается, что сокращается, а что остается
По определению сумма ряда это предел последовательности {S_(n)}
[b]S= lim_(n→∞)S_(n)[/b]=(1/3)*(3/2)= [b]1/2[/b] о т в е т. 1/2
