Задача 36203 Построение прямоугольника. Свойства...
Условие
Вариант 1
1. ABCD — прямоугольник. По данным рисунка 303 найдите величину
угла x.
2. ABCD — прямоугольник, периметр которого равен 8,4 см. Найдите длины
смежных сторон этого прямоугольника, если они относятся как 3 : 4.
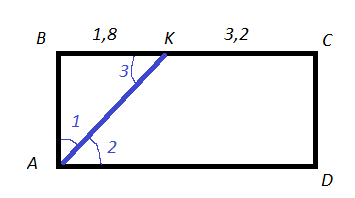
3. ABCD — прямоугольник. Найдите его периметр, если биссектриса угла A
делит сторону BC на два отрезка, длины которых 1,8 см и 3,2 см.
Вариант 2
1. ABCD — прямоугольник. По данным рисунка 304 найдите величину
угла x.
2. ABCD — прямоугольник, периметр которого равен 8,4 см. Найдите длины
смежных сторон этого прямоугольника, если они относятся как 5 : 7.
3. ABCD — прямоугольник. Найдите его периметр, если биссектриса угла C
делит сторону AD на два отрезка, длины которых 3,4 см и 2,6 см.

Решение
x=58^(o) - это внутренние накрест лежащие углы при AB||CD и секущей BD.
2.Пусть k - коэффициент попорциональности
a=3k;
b=4k
Р=2*(a+b)
2*(a+b)=8,4
2*(3k+4k)=8,4
14k=8,4
k=0,6
a=3k=3*0,6=1,8
b=4k=4*0,6=2,4
3. Cм. рис.
∠ 1= ∠ 2 - так как биссектриса делит угол пополам
∠ 2= ∠ 3=это внутренние накрест лежащие углы при BС||АD и секущей АК.
ΔАВК - равнобедренный.
АВ=ВК= [b]1,8[/b]
ВС=BК+КС=1,8+3,2= [b]5[/b]