Задача 36123 ...
Условие
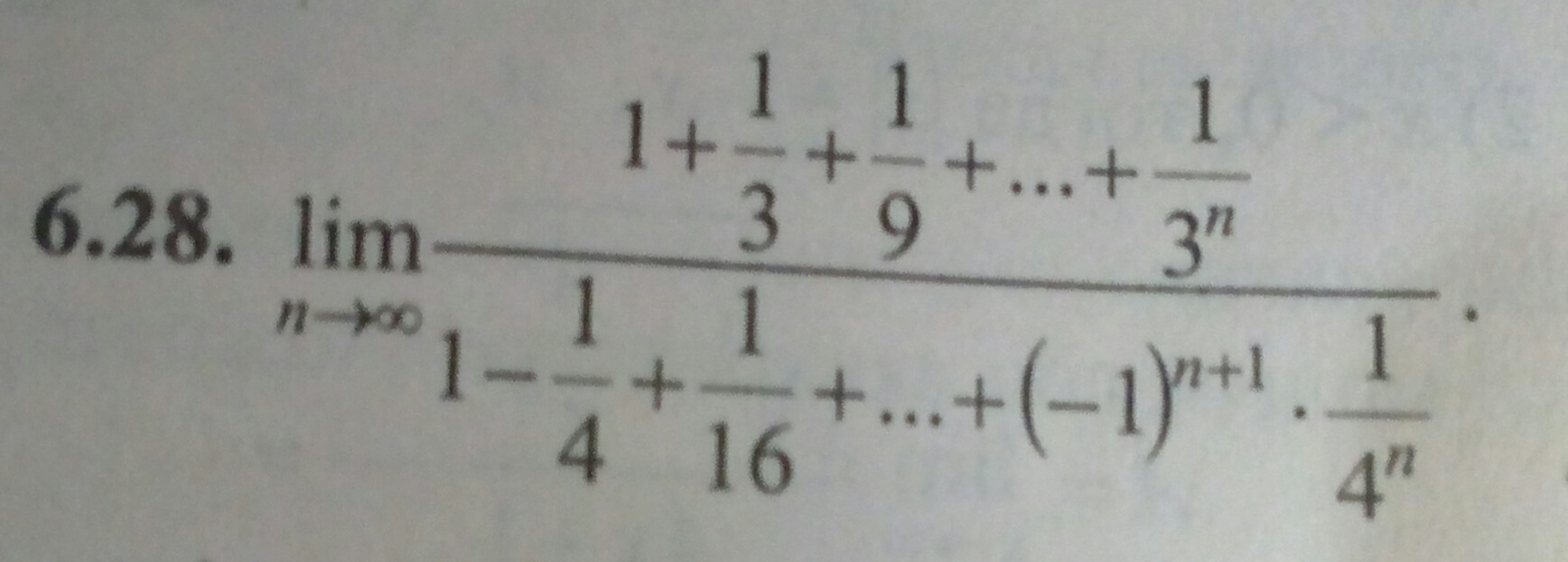
математика ВУЗ
740
Решение
★
S_(n)=b_(1)*(1-q^n)/(1-q)
В числителе получим
1*(1-(1/3)^n)/(1-1/3) →3/2, так как (1/3)^(n)→0 при n→ ∞
В числителе получим
1*(1-(-1/3)^n)/(1-(-1/4) →4/5, при n→ ∞
О т в е т. (3/2)/(4/5)=
