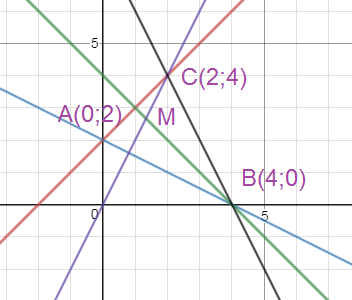
Задача 36080 Помогите, пожалуйста. Составить...

vk492871866

2019-04-19 15:58:56

Помогите, пожалуйста. Составить уравнения сторон треугольника, зная одну его вершину А(0;2), и уравнения высот (ВМ) х+у-4=0 и (СМ) у=2х, где М-точка пересечения высот.

sova

2019-04-19 16:16:47

★

Прямая, перпендикулярная СМ имеет вид:
y=(-1/2)x+b
Подставляем координаты точки А
2=b
[b]y=(-1/2)x+2 - уравнение АВ[/b]

Прямая, перпендикулярная ВМ имеет вид:
y=x+b
Подставляем координаты точки А
2=b
[b]y=х+2 - уравнение АС[/b]

Находим координаты точки B, как точки пересечения высоты ВМ и стороны АВ:
{х+у–4=0
{y=(-1/2)x+2

(-1/2)x+2=-x+4
x=4
y=0
[b]B(4;0)[/b]

Находим координаты точки С, как точки пересечения высоты СМ и стороны АС:
{y=2x
{y=x+2

2x=x+2
x=2
y=4
[b]C(2;4)[/b]
Составляем уравнение стороны ВС, как прямой проходящей через две точки В и С:
y=kx+b

0=4k+b
4=2k+b

k=-2

b=8

[b]y=-2x+8[/b] - уравнение ВС