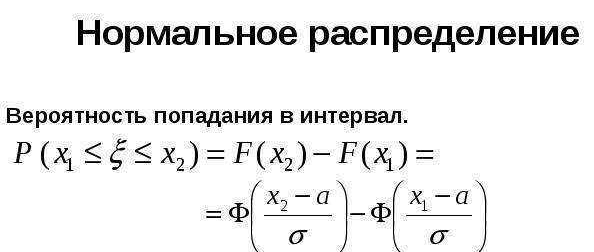Задача 36040 Найти вероятность попадания нормально...

alekseevadaria

2019-04-18 16:51:16

Найти вероятность попадания нормально распределенной случайной величины X в интервале [m]11 < X < 14[/m], если a = 12, D(x) = 4.

sova

2019-04-18 17:32:27

★

a=12
σ=sqrt(D(x))=sqrt(4)=2
x_(2)=14
(x_(2)-a)/σ=(14-12)/2=1
(x_(1)-a)/σ=(11-12)/2=-1/2

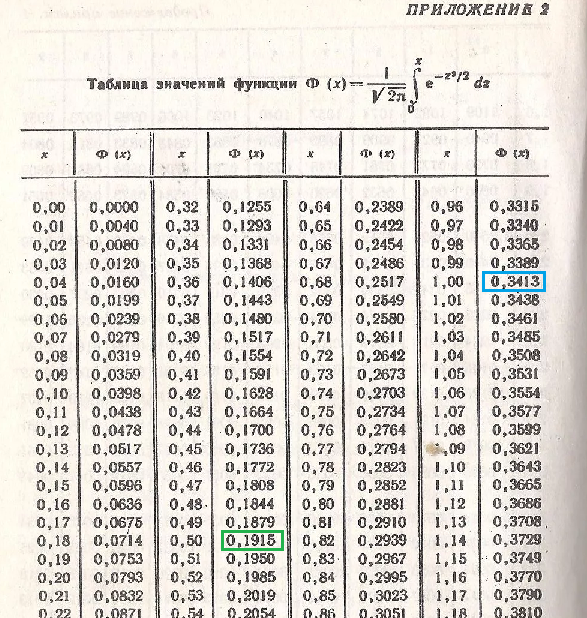
Ф(1)=0,3413

Ф(-1/2)=-Ф(1/2)=-0,1915

P(11<x<14)=Ф(1)-(-Ф(1/2))=Ф(1)+Ф(1/2)=0,3413+0,1915=