Задача 36014 ...
Условие
Задача 1. Найти объём и площадь полной поверхности прямой призмы, боковое ребро которой 9 см, а основание — прямоугольный треугольник с гипотенузой равной 25 см и один из катетов 7 см.
Задача 2. Основание пирамиды — треугольник ABC, у которого AB=8 м, BC=7 м, угол ABC=120°. Высота пирамиды равна 3√3 м. Вычислить объём пирамиды.
Задача 3. В правильной четырехугольной призме S_мп=90 см², S_о_сн=40 см². Вычислить объём призмы.
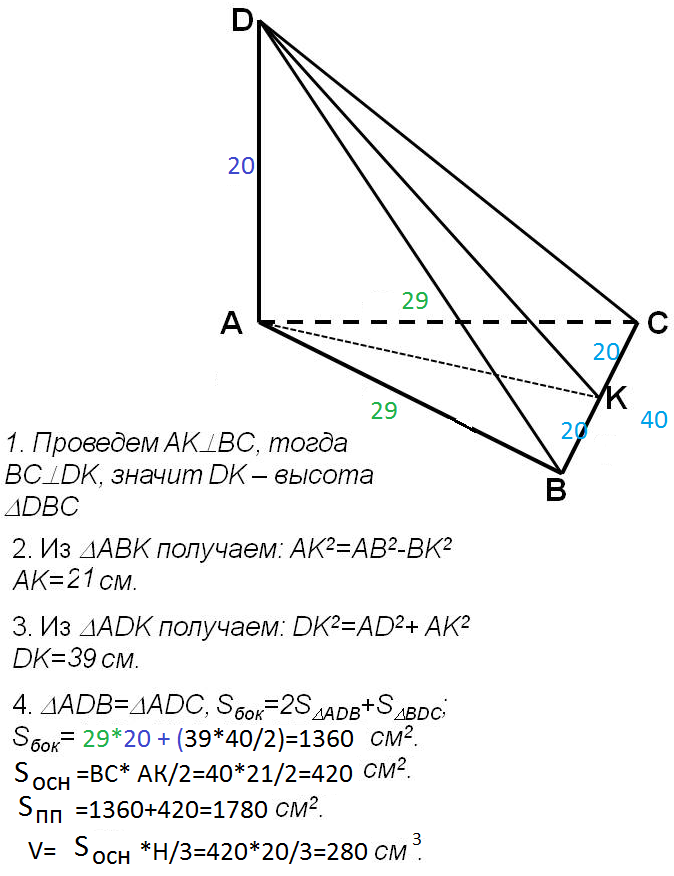
Задача 4. В пирамиде DABC ребро DA перпендикулярно плоскости основания - треугольника ABC. DA=11 см, |AB = AC=25 см, BC=24 см. Найти объём и площадь полной поверхности пирамиды.
Задача 5*.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение
По теореме Пифагора второй катет
sqrt(25^2-7^2)=sqrt((25-7)*(25+7))=sqrt(18*32)=3*8=24 см
V=S_(осн.)*Н=(1/2)*7*24*9=756 кв. см
2.
V_(пирамиды)=(1/3)*S_(осн)*H
Н=3sqrt(3)
S_(осн)=(1/2)AB*BC*sin ∠ ABC=(1/2)*8*7*sqrt(3)/2=14sqrt(3)
V=(1/3)*(14sqrt(3))*3sqrt(3))=42 куб. м
3.
Sпп=Sбп+2Sосн
Sосн=(90-40)/2=25
В основании квадрат, его площадь 25, значит сторона основания а=5
Sбп=Росн*Н=4а*Н=4*5*Н=20Н
По условию
Sбп=40
20Н=40
Н=2
V=Sосн*Н=25*2=50 cм^3
5.
S_(осн)=4*3-1*1=11
S_(бок)=Р_(осн)*5=(4+3+2+1+1+3)*5=70
S_(пп)=70+2*11=92
4.