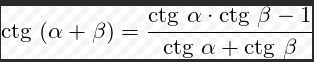Задача 35919 ...

ladykaramel

2019-04-16 15:45:43

ctg(arctg(√3/4) + arctg(3√3/7))

sova

2019-04-16 16:15:24

Обозначим

arctg(sqrt(3)/4)= α ⇒ tg α =sqrt(3)/4; α ∈ (-π/2;π/2)⇒

[b]ctgα=1/tgα=4sqrt(3)/3[/b]

arctg(3sqrt(7)/7)= β ⇒ tg β =3sqrt(7)/7; β ∈ (-π/2;π/2)⇒

[b]ctgβ=1/tgβ=sqrt(7)/3[/b]

ctg( α + β )=(ctg α *ctg β -1)/(ctg α +ctg β ) =

=((4sqrt(21)/3)-3)/(4sqrt(3)+sqrt(7))