Задача 35883 ...

help

15 апреля 2019 г. в 19:47

Вычислить площади фигур, ограниченные линиями:

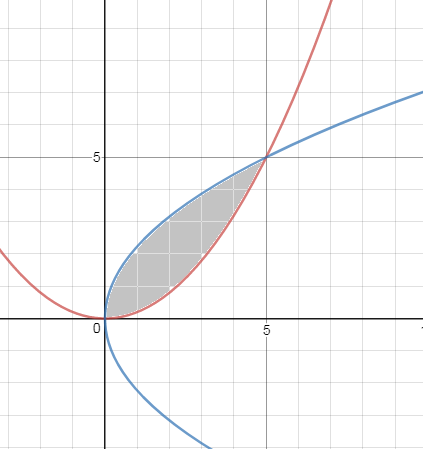
а) 5у = x², y² = 5x;

б) { x = 8cos³(t)
y = 2sin³(t), π/4 ≤ t ≤ 0;

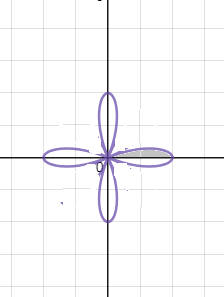
в) ρ = 2cos4φ.

sova

15 апреля 2019 г. в 20:19

★

a) cм. рис.1

y=x²/5 – парабола красным цветом

y=√5x – степенная функция, синим
S= ∫ ⁵₀(√5x–(x²/5))dx=

= (√5·x^3/2/(3/2)–(1/5)·(x³/3) )|⁵₀=

=(2√5/3)·√5³–(1/15)·5³=

=(50/3)–(25/3)= 25/3

б)
S= ∫ t2t1y(t)·x`(t)dt

y(t)=8cos³t
x(t)=2sin³t
x`(t)=2·3·sin<sup>2</sup>t·(sint)`=6sin²tcost

S= ∫ ^π/4₀8·cos³t·6sin²tcostdt=

=48 ∫ ^π/4₀cos⁴t·sin²tdt= понижаем степени

=48 ∫ ^π/4₀((1+cos2t)/2)²·(1–cos2t)dt/2=

=6 ∫ ^π/4₀((1–cos²2t)·(1+cos2t)dt=

=6 ∫ ^π/4₀((1–cos²2t+cos2t–cos³2t)dt=

=6 ∫ ^π/4₀((1–(1+cos4t)/2+cos2t–(1–sin²2t)·cos2t)dt=

=6· ((t/2)–(1/8)sin4t +(1/2)(sin³2t)/3 )|^π/4₀=

=6π/8= 3π/4

в)

S=(1/2) ∫ ^β _α ρ²( φ )d φ

cos4φ ≥0

–π/2 ≤4φ≤π/2

–π/8 ≤φ≤π/8

4 лепестка ( см. рис.2),
считаем площадь половины лепестка и умножаем на 8

S=(1/2) ·8·∫ ^π/8₀ (2cos4φ)²dφ=

=16·∫^π/8₀ (cos²4φ)dφ= понижаем степень

=16·∫ ^π/8₀ ((1+сos8φ)/2)dφ=

=8·( φ +(1/8)sin8 φ )|^π/8₀ =

=8·(π/8)= π