Задача 35873 ...
Условие
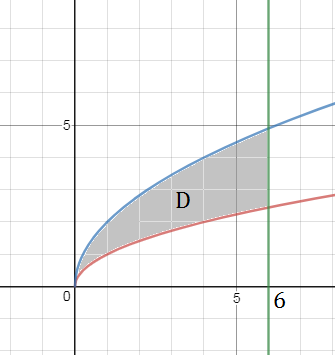
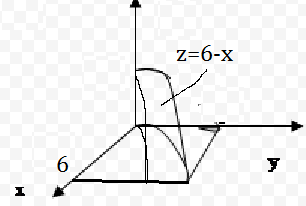
z = 0, y = √x, y = 2√x, x + z = 6.
математика ВУЗ
389
Решение
★
D: 0 ≤ х ≤ 6
sqrt(x) ≤ y ≤ 2sqrt(x)
z=6-x ⇒ f(x;y)=6-x
V= ∫ ^(6)_(0) [b]([/b]∫ ^(2sqrt(x))_(sqrt(x))(6-x)dy [b])[/b] dx=
=∫ ^(6)_(0) (6-x)*y|^(2sqrt(x))_(sqrt(x))dx
=∫ ^(6)_(0) (6-x)*(2sqrt(x)-sqrt(x))dx=
= ∫ ^(6)_(0) (6sqrt(x)-xsqrt(x))dx=
=(6*x^(3/2)/(3/2)- x^(5/2)/(5/2))|^(6)_(0)=
=6*(2/3)*6^(3/2)-(2/5)*6^(5/2)=
=4*sqrt(6^3)-(2/5)*sqrt(6^5)= [b]9,6sqrt(6)[/b]