Задача 35871 Задание на картинке...
Условие
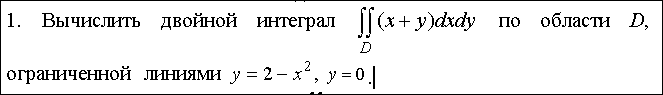
математика ВУЗ
519
Решение
★
-sqrt(2) ≤ x ≤ sqrt(2)
0 ≤ y ≤ 2-x^2
∫ ∫_(D)(x+y)dxdy=∫^(sqrt(2)_(-sqrt(2)) [b]([/b]∫^(2-x^2)_(0)(x+y)dy [b])[/b]dx=
=∫^(sqrt(2)_(-sqrt(2)) [b]([/b]xy+(y^2/2) [b])[/b]|^(2-x^2)_(0)dx=
=∫^(sqrt(2)_(-sqrt(2)) [b]([/b]x*(2-x^2)+((2-x^2)^2/2) [b])[/b]dx=
=∫^(sqrt(2)_(-sqrt(2)) (2x-x^3+(4-4x^2+x^4)/2)dx=
=((2x^2/2)- (x^4/4) +2x-(2x^3/3)+(x^5/10))|^(sqrt(2)_(-sqrt(2))=
=(2-2) -(1/4) (4-4)+2*(sqrt(2)-(-sqrt(2)))-(2/3)*(2sqrt(2)+2sqrt(2))+(1/10)*(4sqrt(2)+4sqrt(2))=
=4sqrt(2)-8sqrt(2)/3 +8sqrt(2)/10= [b]32sqrt(2)/15[/b]