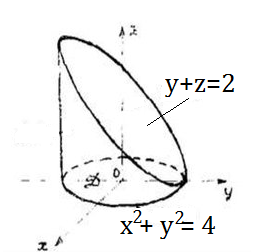Задача 35814 1. Вычислить объем тела, ограниченного...

qwe4

13 апреля 2019 г. в 22:58

1. Вычислить объем тела, ограниченного поверхностями

x² + y² = 4, y + z = 2 и z = 0.

sova

13 апреля 2019 г. в 23:10

★

V= ∫ ∫ _{по окружности x²+y²=4}(2–y)dxdy=

=переходим к полярным координатам

x=rcos φ ; y=rsin φ
dxdy=rdrd φ

= 2∫ ^π₀ ∫ ²₀(2–rsin φ )rdrd φ =

=2 ∫ ^π₀ ∫ ²₀((2r–r²sin φ )dr)d φ =

=2∫ ^π₀((2r²/2)–(r³/3)sin φ )|²₀d φ =

=2∫ ^π₀(4–(8/3)sin φ )d φ =

=2·(4φ +(8/3)cos φ )|^π₀=8π+(16/3)(cosπ–cos0)=

=8π–(32/3)