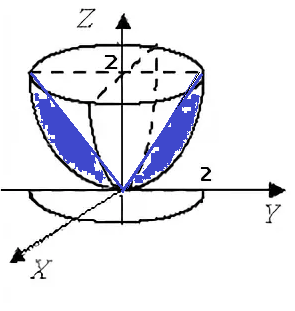
Задача 35796 № 9.3.156 ...

bolanebyla

2019-04-13 13:46:27

№ 9.3.156

sova

2019-04-13 23:47:12

Поверхности пересекаются по
z^2=2z ⇒ z=0 или z=2

При z=0
область D: x^2+(y^2/4)=4 ⇒ (x^2/4)+(y^2/16)=1 - эллипс

V тела, заключенного между параболоидом и конусом -

Из объема параболоида вычитаем объем конуса:

V= ∫ ∫ _(по эллипсу (x^2/4)+(y^2/16)=1) ((x^2+(y^2/4))/2 - sqrt(x^2+(y^2/4)))dxdy

Так как область D - эллипс, переходим к обощенным полярным координатам

x=rcos φ
y=2rsin φ
dxdy=2drd φ