Задача 35732 ...
Условие
∛(x⁶ - 26) + 2∛(x⁶ - 26) = 3;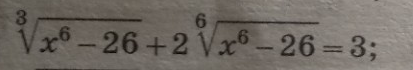
математика 10-11 класс
1031
Все решения
t^2 +2t -3=0
D=16
t=-3; t=1
(x^6-26)^(1/6)=- 3 нет решений
или
(x^6-26)^(1/6)=1
x^6-26=1
x^6=27
x^2=3
[b]x= ± sqrt(3)[/b]
