Задача 35711 [m]\sqrt{x-2} + \sqrt{4-x} = x^2 - 6x +...
Условие
[m]\sqrt{x} - \sqrt{x+1} - \sqrt{x+4} + \sqrt{x+9} = 0[/m]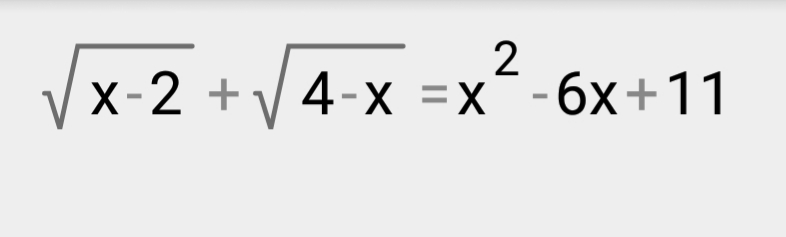
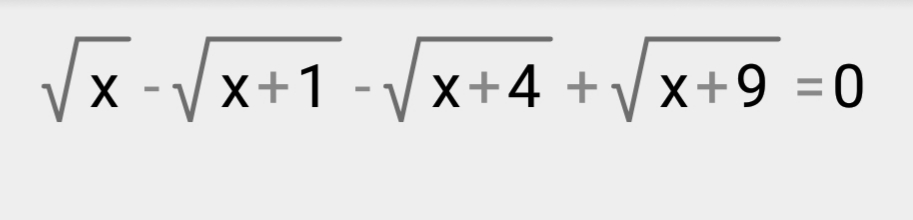
Решение
{x-2 ≥ 0 ⇒ x ≥ 2
{4-x ≥ 0 ⇒ x ≤ 4
x ∈ [2;4]
возводим обе части в квадрат
x^2-6x+11>0 при любом х, D <0
x-2 +2*sqrt((x-2)*(4-x))+4-x=(x^2-6x+11)^2
2*sqrt((x-2)*(4-x))+2=(x^2-6x+11)^2
2*sqrt(-x^2+6x-8)+2=(x^2-6x+11)^2
замена
-x^2+6x-8=t
x^2-6x+11=3-t
2sqrt(t)+2=t^2
2sqrt(t)=t^2-2
{4t=t^4-4t^2+4
{t^2-2≥
t^4-4t^2-4t+4=0
2.
sqrt(x)+sqrt(x+9)=sqrt(x+1)+sqrt(x+4)
x+2*sqrt(x)*sqrt(x+9)+x+9=x+1+2*sqrt(x+1)*sqrt(x+4)+x+4
2*sqrt(x)*sqrt(x+9)+4=2*sqrt(x+1)*sqrt(x+4)
sqrt(x)*sqrt(x+9)+2=sqrt(x+1)*sqrt(x+4)
[b]sqrt(x+1)*sqrt(x+4)-sqrt(x)*sqrt(x+9)=2[/b]
Умножаем на
sqrt(x+1)*sqrt(x+4)+sqrt(x)*sqrt(x+9)
2*(sqrt(x+1)*sqrt(x+4)+sqrt(x)*sqrt(x+9))=(х+1)*(х+4)-х*(х+9)
[b](sqrt(x+1)*sqrt(x+4)+sqrt(x)*sqrt(x+9))=2-2х[/b]
Складываем
два уравнения
2sqrt(x+1)*sqrt(x+4)=4-2х
Возводим в квадрат: