Задача 35658 ...
Условие
2. ∛(x + 1) + ∛(x + 2) + ∛(x + 3) = 0
3. (x - √(x^2 - 1))^3 × (x + √(x^2 - 1))^5 = 1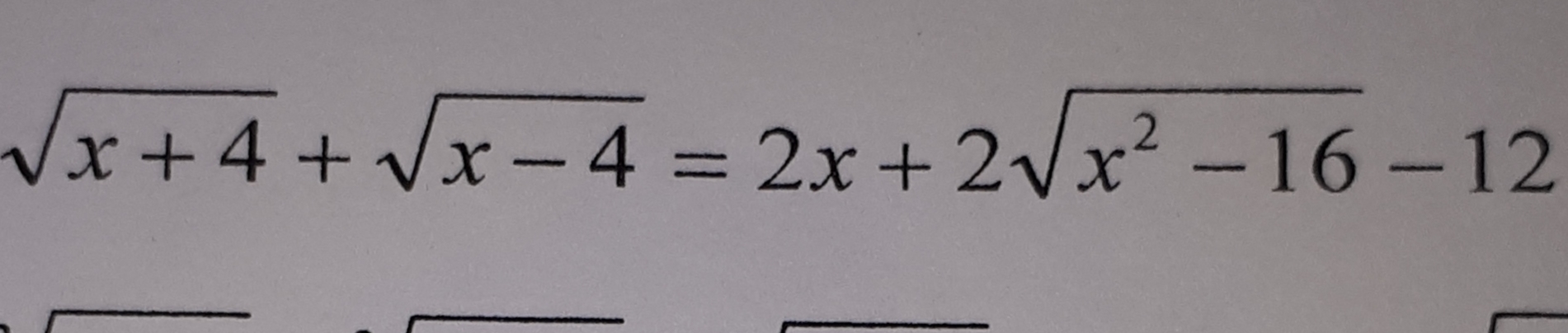
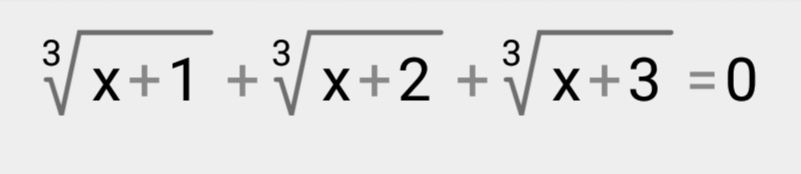
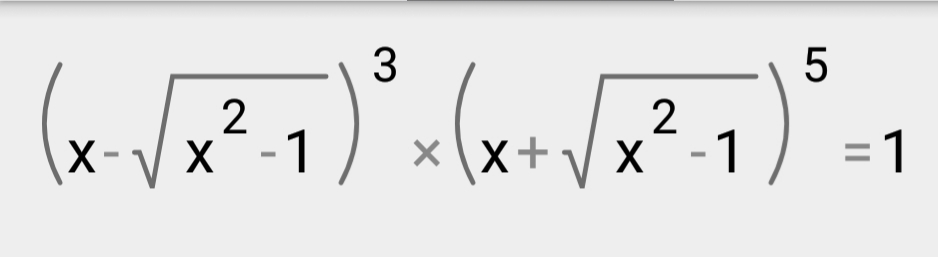
Решение
{x+4 ≥0 ⇒ x ≥ -4
{x-4≥0 ⇒ x ≥ 4
{x^2-16≥0 ⇒ x≤ -4 или x ≥ 4
х ∈ [4;+ ∞ )
Замена переменной:
sqrt(x+4)+sqrt(x-4)=t
t≥0 на ОДЗ как сумма неотрицательных выражений
Возводим в квадрат
x+4+2sqrt((x+4)*(x-4))+x-4=t^2
2x+2sqrt(x^2-16)=t^2
Уравнение:
t=t^2-12=0
t^2-t-12=0
D=49
t=-3 или t=4
t=-3 посторонний корень.
sqrt(x+4)+sqrt(x-4)=4
Возводим в квадрат
sqrt(x^2-16)=16-2x
sqrt(x^2-16)=8-x
Возводим в квадрат
x^2-16=64-16x+x^2
16x=80
[b]х=5[/b]
2)
∛(х+1) + ∛(х+2) =- ∛(х+3)
Возводим в куб:
x+1+3*∛(x+1)^2*∛(x+2) +3*∛(x+1)*∛(x+2)^2 +x+2=- x - 3
3*∛(x+1)^2*∛(x+2) +3*∛(x+1)*∛(x+2)^2= - 3x - 6
∛(x+1)*∛(x+2)*(∛(x+1)+∛(x+2)= - x - 2
Так как по условию
∛(x+1)+∛(x+2) = - ∛(х+3)
∛(x+1)*∛(x+2)*(-∛(х+3)) =- x - 2
Возводим в куб
(x+1)*(x+2)*(x+3)=(x+2)^3
(x+1)*(x+2)*(x+3)-(x+2)^3=0
(x+2)*(x^2+4x+3-x^2-4x-4)=0
(х+2)*(-1)=0
[b]x=-2[/b]
3)
(x-sqrt(x^2-1))^3*(x+sqrt(x^2-1))^3*(x+sqrt(x^2-1))^2=1
(x^2-(x^2-1))^3*(x+sqrt(x^2-1))^2=1
1^3*(x+sqrt(x^2-1))^2=1
(x+sqrt(x^2-1))^2=1
x^2+2x*sqrt(x^2-1)+x^2-1=1
2x*sqrt(x^2-1)=2-2x^2
x*sqrt(x^2-1)=1-x^2
...
[b]x= ± 1[/b]