Задача 35633 ...
Условие
2. ⁵√((5x + 2)^3) - 16/⁵√((5x + 2)^3) = 6
3. ³√(1 + √x) + ³√(1 - √x) = 2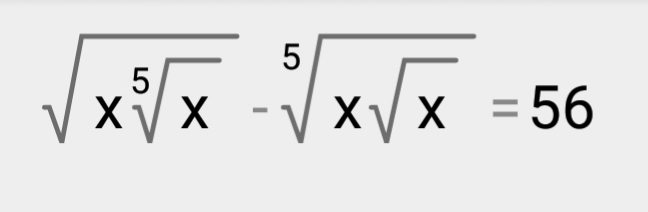
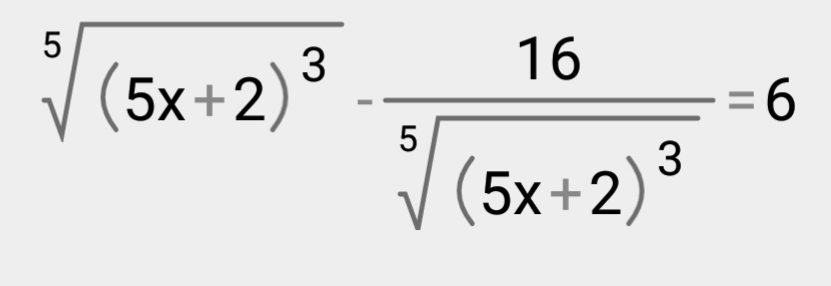
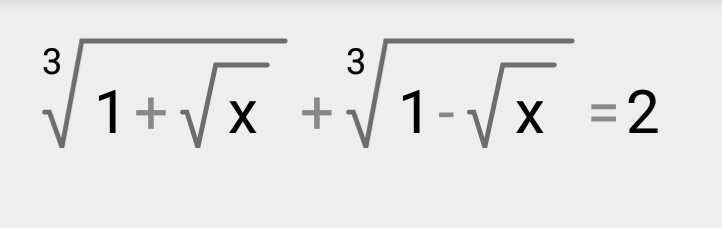
Решение
Замена
x^(3/10)=t
t^2-t-56=0
D=1+224=225
t=-7 или t=8
Обратно:
x^(3/10)=-7 не имеет решения, справа только неотрицательные значения
x^(3/10)=8
x=2^(10)= [b]1024[/b]
2)
Замена
(5х+2)^(3/5)=t
t - (16/t)=6
t^2-6t-16=0
D=36+64=100
t=-2 или t=8
Обратный переход
(5х+2)^(3/5)=-2
или
(5х+2)^(3/5)=8
5х+2=(-2)^(5/3)или 5х+2=(8)^(5/3)
5х=-2∛4- 2 или 5х=8∛64- 2
x= [b](-2∛4- 2)/5 [/b] или х=(32-2)/5= [b]6[/b]
3)
Возводим в куб:
1+sqrt(x)+3*∛(1+sqrt(x))^2*∛(1-sqrt(x)) +3*∛(1+sqrt(x))*∛(1-sqrt(x))^2 +1-sqrt(x)=8
3*∛(1+sqrt(x))^2*∛(1-sqrt(x)) +3*∛(1+sqrt(x))*∛(1-sqrt(x))^2 =6
∛(1+sqrt(x))*∛(1-sqrt(x))* [b](∛(1+sqrt(x))+∛(1-sqrt(x)))[/b]=2
∛(1+sqrt(x))*∛(1-sqrt(x))* [b]2[/b]=2
∛(1+sqrt(x))*∛(1-sqrt(x))=1
(1+sqrt(x))*(1-sqrt(x))=1
1-x=1
[b]x=0[/b]