Задача 35544 982 , решение ) ...

vk382826215

2019-04-08 21:09:18

982 , решение )

sova

2019-04-09 14:06:11

Это угол ACD.
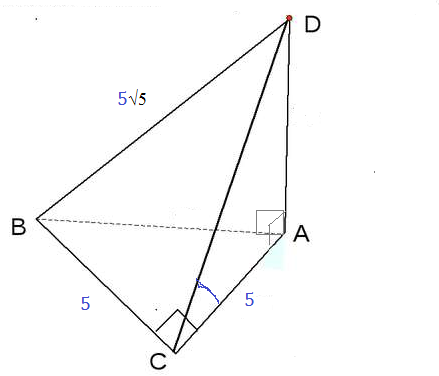
AC ⊥ CB
По теореме о трех перпендикулярах
DC ⊥ CB

Из прямоугольного треугольника DCB
DC^2=DB^2-BC^2=(5sqrt(5))^2-5^2=75-25=50
DC=5sqrt(2)

Из прямоугольного треугольника ACD:
cos ∠ ACD=AC/DC=5/5sqrt(2)=1/sqrt(2)
∠ ACD=45 градусов