Задача 35502 Типовой расчет Исследование функций и их...

vk185128151

8 апреля 2019 г. в 00:20

Типовой расчет
Исследование функций и их графиков
СОДЕРЖАНИЕ ЗАДАНИЯ

Требуется исследовать две заданные функции (под номерами N1 и N2) методом дифференциального исчисления и начертить их график. Для этого рекомендуется:
1. Найти область существования и точки разрыва функции, ее односторонние пределы в этих точках.
2. Выяснить не является ли функция четной или нечетной.
3. Найти точки пересечения графика функций с осями координат.
4. Найти точки экстремума и интервалы убывания и возрастания функции.
5. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции.
6. Определить асимптоты графика функции.
7. Построить график функции.
Если их окажется недостаточно, то следует найти еще несколько точек графика функции, исходя из уравнения линии.

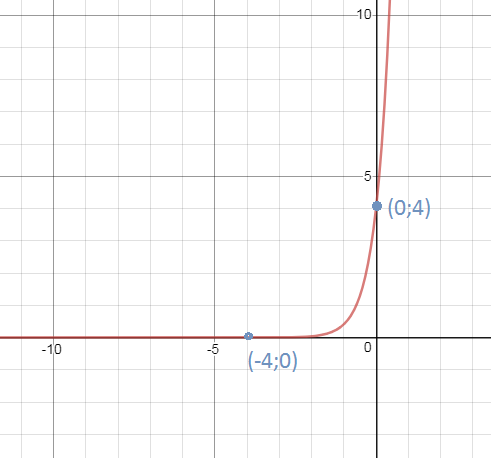
13. y = (x + 4)e^2x

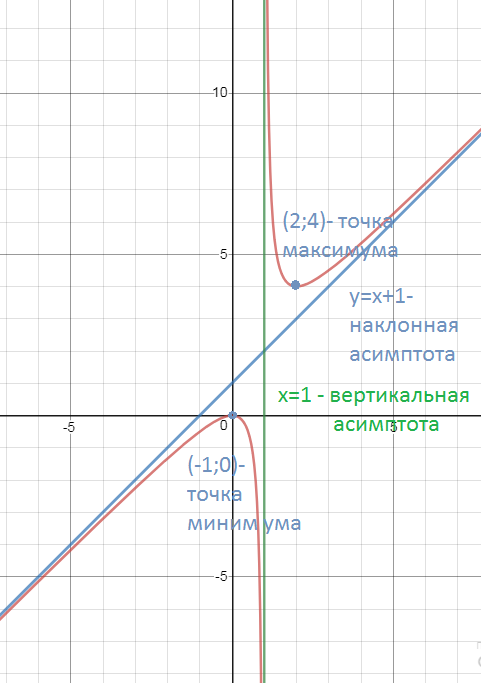
73. y = (x²) / (x – 1)

sova

8 апреля 2019 г. в 09:14

★

13
Область определения функции
(–∞;+∞)

2. Функция не является ни четной, ни нечетной, так как
y(–x)=(–x+4)·e^–2x=–(x–4)·e^–2x
y(–x) ≠ y(x)
y(–x) ≠ –y(x)

3. Точки пересечения с осями координат
y=0 ⇒ x=–4
(–4;0)– точка пересечения c осью Оy
x=0
y=4e⁰=4
(0;4) точка пересечения c осью Оx

4.
y`=(x+4)`·e^2x=(x+4)·(e^2x)`=e<sup>2x</sup>+(x+4)·e<sup>2x</sup>·(2x)`=

=(1+2x+8)·e^2x

y`=0
2x+9=0
x=–9/2

x=–9/2 – точка минимума, производная меняет знак с – на +

y`<0 на (–∞;–9/2)
Функция убывает на (–∞;–9/2)


y`>0 на (–9/2;+ ∞)
Функция возрастает на (–9/2;+ ∞)

y``=2·e^2x+(2x+9)·e^2x·2=e^2x·(2+4x+18)=4·(x+5)·e^2x

y``=0
x=–5

y`` < 0 на (–∞;–5)
Кривая выпукла вверх на (–∞;–5)

y``>0 на (–5;+ ∞)

Кривая выпукла вниз на (–5;+ ∞)


73.
1.Область определения функции
(–∞;1)U(1;+∞)

2. Функция не является ни четной, ни нечетной, так как
y(–x)=(–x)²/((–x)–1) =x²/(–x–1)=–x²/(x+1)
y(–x) ≠ y(x)
y(–x) ≠ –y(x)

3. Точки пересечения с осями координат
y=0 ⇒ x=0
(0;0)– точка пересечения и осью Ох и с осью Оу.

4. Асимптоты

x=1 – вертикальная асимптота
lim_x→1–0= – ∞
lim_x→1+0= + ∞

y=x+1– наклонная асимптота:
k=lim_x→∞f(x)/x=lim_x→∞(x²)/(x·(x–1)=1
b=lim_x→∞(f(x)–kx)=lim_x→∞(f(x)–x)=lim_x→∞(x²–x²+x)/(x–1)=1

5.Интервалы монотонности и экстремумы

y`=((x<sup>2</sup>)`·(x–1)–(x–1)`·x<sup>2</sup>)/(x–1)<sup>2</sup>
y`=(2x²–2x–x²)/((x–1)²
y`=(x<sup>2</sup>–2x)/(x–1)<sup>2</sup>
y`=0
x²–2x=0
x·(x–2)=0
x=0 или х=2
Расставляем знак производной:
_+__ (0) _–__ (1) _–_₂ _+__

х= 2 – точка минимума, производная меняет знак с – на +
х=0 – точка максимума, производная меняет знак с + на –

Функция возрастает на ( – ∞;0) (2;+ ∞)
убывает на ( 0;1) и на (1;2)

6.Интервал выпуклости, точки перегиба

y``=((x²–2x)`·(x–1)<sup>2</sup> – ((x–1)<sup>2</sup>)`·(x²–2x))/(x–1)⁴

y``=(2x²–2x–2x+2–2x²+4x)/(x–1)³

y``=2/(x–1)³

y`` < 0 на (–∞;1)
Кривая выпукла вверх на (–∞;1)

y``>0 на (1;+ ∞)

Кривая выпукла вниз на (1;+ ∞)