Задача 35429 ...
Условие
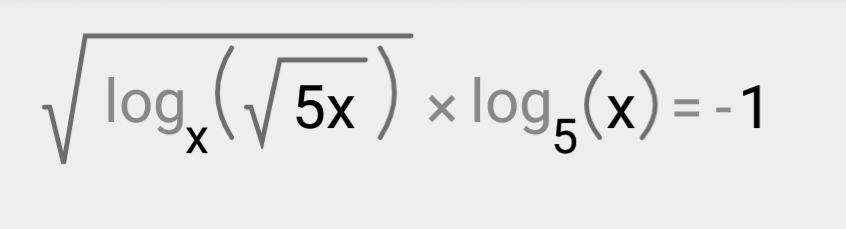
математика 10-11 класс
556
Решение
★
{x>0
{x ≠ 1
{log_(x)sqrt(5x)≥ 0 ⇒ применяем метод рационализации
(x-1)*(sqrt(5x)-1)≥ 0
x ∈ (0;1/5] U (1;+ ∞)
log_(x)sqrt(5x)=(log_(x)sqrt(5)+log_(x)sqrt(x))=(1/2)log_(x)5+(1/2)
Замена переменной:
log_(x)5=t
t ≠0
log_(5)x=1/t
sqrt((1/2)t+(1/2))*(1/t)=-1
Возводим в квадрат при условии, что t < 0
((1/2)t+(1/2))*(1/t^2)=1
2t^2-t-1=0
t=-1/2 или t=1 ( не удовл. условию t<0)
log_(x)5=-1/2
x^(-1/2)=5
1/sqrt(x)=5
x=1/25 ∈ ОДЗ
О т в е т. 1/25