Задача 35427 1. При всех допустимых a и b найти...

vk204995743

5 апреля 2019 г. в 18:24

1. При всех допустимых a и b найти численное значение выражения

[m]
\left( \frac{9a^2 - 16b^2}{4b + 3a} - \frac{a^2b - 3ab^2}{ab} \right)^2 : \left( \frac{6ab - 8a^3 - b^3}{2a - b} \right).
[/m]

2. Решить неравенство

[m]
\frac{(x - 3)^4(x + 1)^3}{(x - 2)^2 (x + 2)} \leq 0.
[/m]

3. (16 баллов) В прямоугольном треугольнике ABC из вершины прямого угла C проведены медиана CM и высота CH. Найти отношение AH : AM, если CM : CH = 5 : 4 и точка H находится между точками A и M.

4. (16 баллов) Антикварный магазин продал картину со скидкой в 10% по сравнению с первоначально назначенной ценой и получил при этом 8% прибыли. Сколько процентов прибыли магазин предполагал получить первоначально?

5. (20 баллов) Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк 1/6 часть от всей суммы, которую он должен был банку к этому времени. А еще через год в счет полного погашения кредита фермер внес в банк сумму, на 20% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

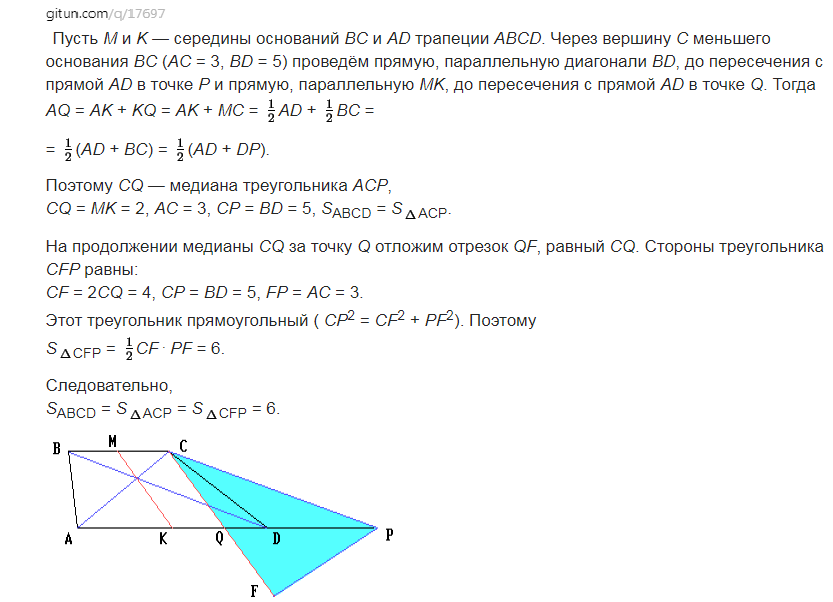
6. (20 баллов) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции.

sova

5 апреля 2019 г. в 20:39

1.

В первой скобке
9a²–16b²=(3a–4b)(3a+4b)

(9a²–16b²)/(4b+3a)= (3a–4b)(3a+4b)/(4b+3a)=3a–4b

(a²b–3ab²)=ab(a–3b)

(a²b–3ab²)/ab=ab(a–3b)/ab=a–3b

(3a–4b–(a–3b))²=(3a–4b–a+3b)²= (2a–b)²


Во второй скобке:
8a³–b²=(2a–b)·(4a²+2ab+b²)

(8a³–b²)/(2a–b)=(2a–b)·(4a²+2ab+b²)/(2a–b)=4a²+2ab+b²

6ab– (8a³–b²)/(2a–b)=6ab–4a²–2ab–b²=4ab–4a²–b²=

=–(4a²–4ab+b²)= –(2a–b)²

Делим и получаем (–1)

О т в е т. –1

2.
Применяем метод интервалов.
Находим нули числителя:
x–3=0; x+1=0
x=3; x=–1
Обозначаем сплошным кружком ( квадратная скобка на рис.)

Нули знаменателя:
x–2=0; x+2=0
x=2; x=–2
Обозначаем пустым кружком (круглая скобка)

__+_ (–2) __+_ [–1] __–__ (2) __+_ [3] __+__

О т в е т. [–1;2) U{–3}

3.

В прямоугольном треугольнике – середина гипотенузы центр описанной окружности,
СM=AM=BM

Обозначим k – коэффициент пропорциональности, тогда
CM=5k,CH=4k и CM:CH=5:4

По теореме Пифагора из Δ CMH
HM=3k

Так как AM=BM=CM=5k
то AH=2k; AB=10k

AH:AM=2:10= 1:5 – о т в е т.

4.

Пусть взял х руб. под p%

Через год начислены проценты, т.е должен банку
x+0,01px=x·(1+0,01p)

Погасил

(1/6)·x(1+0,01p)

На конец года долг составил (5/6)·х·(1+0,01p)

На остаток начислены проценты и долг составил

(5/6)·x·(1+0,01p)²

Вернул банку на 20% больше, чем взятый кредит, т.е 1,2х

Уравнение
(5/6)·x·(1+0,01p)²=1,2x

(1+0,01p)²=36/25

1+0,01p=6/5

0,01p=0,2

p=20%