Задача 35408 ...
Условие
математика ВУЗ
478
Решение
★
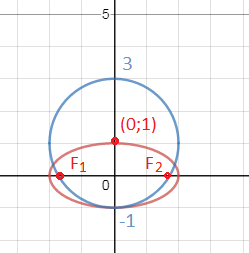
a=2; b=1
Верхняя вершина (0;1)
a>b, значит
b^2=a^2-c^2
c^2=a^2-b^2=2^2-1=3
c=sqrt(3)
Фокусы в точках F_(1) (-sqrt(3);0) и F_(2)(sqrt(3);0)
Уравнение окружности с центром (x_(o);_(o)) и радиусом R
имеет вид:
(x-x_(o))^2+(y-y_(o))^2=R^2
По условию центр окружности в точке (0;1)
Тогда уравнение окружности:
x^2+(y-1)^2=R^2
По условию
точки F_(1) (-sqrt(3);0) и F_(2)(sqrt(3);0)
лежат на окружности, значит координаты точек удовлетворяют уравнению:
sqrt(3)^2+(0-1)^2=R^2
R^2=4
R=2
О т в е т. [b]x^2+(y-1)^2=4[/b]