Задача 35405 ...

vk116113879

5 апреля 2019 г. в 13:31

Контрольные варианты к задаче 1

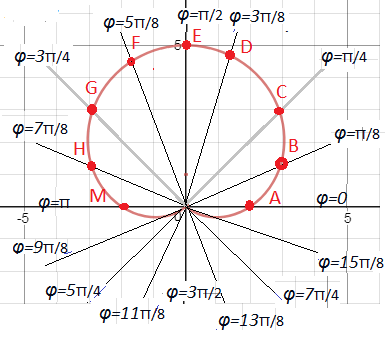
Дано уравнение линии ρ = f(φ) в полярной системе координат. Определить точки, лежащие на линии, в промежутке 0 < φ < 2π. Шаг взять равным π/8. Построить линию. Записать уравнение линии в декартовой системе координат.

1. ρ = sin 3φ + 2. 2. ρ = cos 2φ − 2.

sova

5 апреля 2019 г. в 14:50

★

ρ=3sinφ+2

φ =0⇒ sin0=1
ρ=3·0+2=2

На луче φ =0 откладываем расстояние ρ=2
получаем точку А (0;2)

φ =π/8⇒
ρ=


φ =π/4⇒sin(π/4)=√2/2 ≈0,7
ρ=3·sin(π/4)+2≈ 3·0,7+2=4,1
На луче φ =π/4 откладываем расстояние ρ≈4,1
получаем точку С (π/4; 4,1)

φ =3π/8⇒
ρ=

φ =π/2⇒sin(π/2)=1
ρ=3·sin(π/2)+2= 3·1+2=5
На луче φ =π/2 откладываем расстояние ρ=5
получаем точку Е (π/2;5)

φ =5π/8⇒
ρ=

φ =3π/4⇒sin(3π/4)=√2/2 ≈0,7
ρ=3·sin(3π/2)+2≈ 3·0,7+2=4,1
На луче φ =3π/4 откладываем расстояние ρ≈4,1
получаем точку G (3π/4; 4,1)

φ =7π/8⇒
ρ =


φ =π⇒ sinπ=0
ρ = 3·0+2=2
На луче φ =π откладываем расстояние ρ=2
получаем точку M (π; 2)

и так далее

Переход от полярной системы координат к декартовой

x=ρ·cos φ
y=ρ·sin φ
x²+y²=ρ²⇒ ρ=√x²+y²

sin φ φ =y/ρ=y/√x²+y²



Подставляем в данное уравнение:

√x²+y²=3·y/√x²+y² + 2

x²+y²=3y+2√x²+y²

(x²+y²–3y)=2√x²+y²

Возводим в квадрат

(x²+y²–3y)²=4(x²+y²) уравнение линии в декартовой системе координат