Задача 35403 ...
Условие
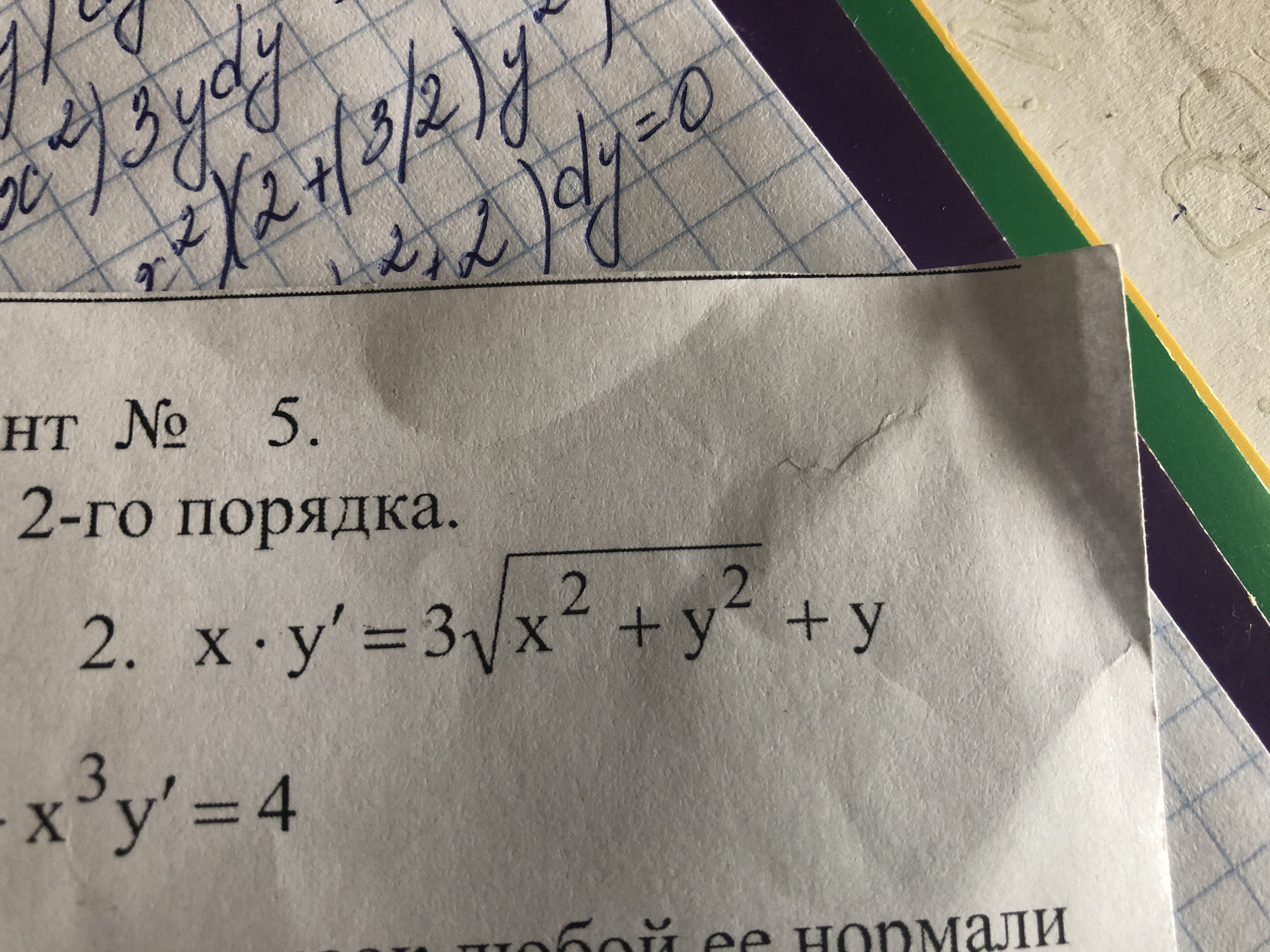
предмет не задан
387
Все решения
y`=3sqrt(1+(y/x)^2) + (y/x)
Уравнение имеет вид:
y`= φ (y/x)
Значит, это однородное уравнение.
Решают заменой
y/x=u
y=xu
y`=x`·u+x·u`
x`=1 так как х – независимая переменная
u+x·u`=3sqrt(1+u^2)+u
x·u`=3sqrt(1+u^2) – уравнение с разделяющимися переменными
u`=du/dx
x*du=3sqrt(1+u^2)dx
du/sqrt(1+u^2)=3dx/x
Интегрируем:
∫ du/sqrt(1+u^2)= ∫ 3dx/x
ln|u+sqrt(1+u^2)|=3ln|x|+lnC
u+sqrt(1+u^2)=Cx^3
(y/x)+sqrt(1+(y/x)^2)=Cx^3
[b]y+sqrt(x^2+y^2)=Cx^4[/b]- о т в е т.