Задача 35277 log3(sin3x-sinx) = 2log9(17sin2x)-1...
Условие
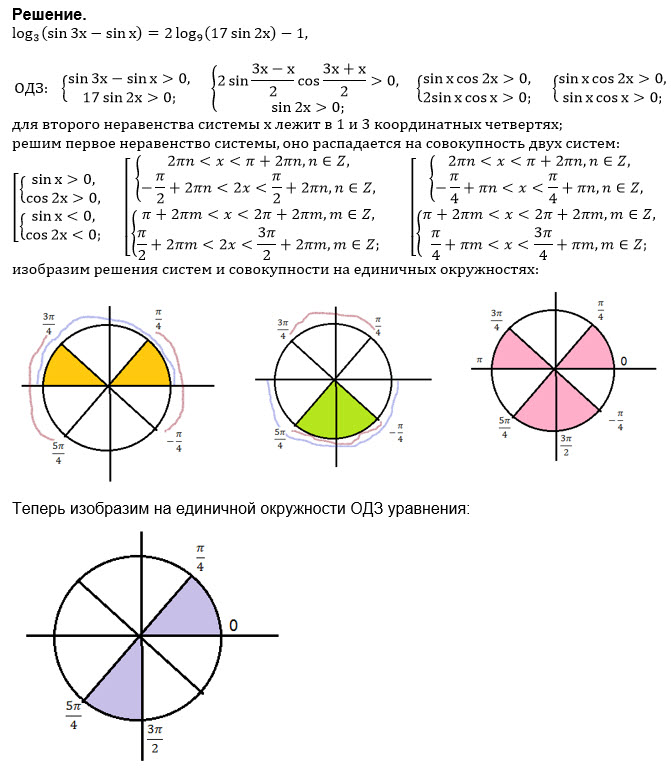
Все решения
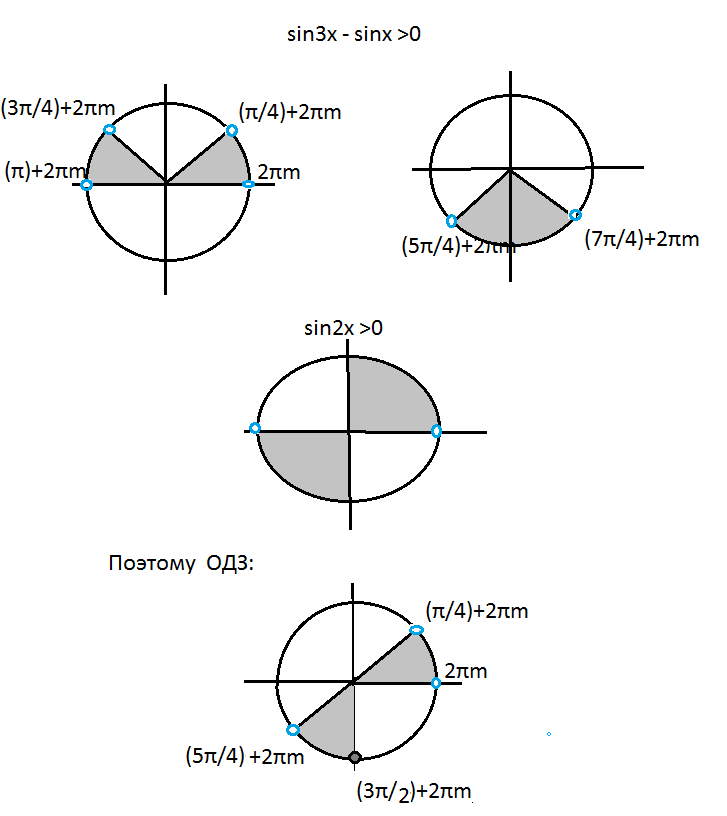
{sin3x-sinx>0⇒ 2sinx*cos2x>0
{17sin2x>0 ⇒ sin2x>0⇒ x в первой или третьей четверти
Решаем первое неравенство:
sinx*cos2x>0⇒
Произведение двух множителей положительно, когда множители имеют одинаковые знаки:
(1) оба положительны
{sinx>0⇒ 2πn< x < π+2πn, n∈ Z
{cos2x>0⇒(-π/2)+2πm< 2x < (π/2)+2πm, m∈ Z⇒
(-π/4)+πm< x < (π/4)+πm, m∈ Z
[b]0+2πm< x < (π/4)+2πm, m∈ Z
или
(3π/4)+2πm< x < π+2πm, m∈ Z[/b]
рис. 1
(2) оба отрицательны
{sinx<0⇒ π+ 2πn< x < 2π+2πn, n∈ Z
{cos2x<0⇒(π/2)+2πm< 2x < (3π/2)+2πm, m∈ Z⇒
(π/4)+πm< x < (3π/4)+πm, m∈ Z
[b](5π/4)+2πm< x < (7π/4)+2πm, m∈ Z[/b]
рис.2
C учетом второго неравенства системы для ОДЗ: sin2x >0
получаем
ОДЗ:
[b]x∈ (0+2πm; (π/4)+2πm) U ((5π/4)+2πm; (3π/2)+2πm]m∈ Z[/b]
cм. рис. 3
Так как по свойствам логарифма:
log_(9)(17sin2x)=log_(3^2)(17sin2x)=(1/2)log_(3)(17sin2x)
1=log_(3)3
log_(3)(sin3x-sinx)=log_(3)(17sin2x)-log_(3)3
log_(3)(sin3x-sinx)=log_(3)((17sin2x)/3)
В силу строгого возрастания логарифмической функции с основанием 3:
если значения функции равны, то и аргументы равны:
sin3x-sinx=(17sin2x)/3
3*(2sinx*cos2x)=17*2sinx*cosx
6sinx*cos2x-34sinx*cosx
2sinx*(3cos2x-17cosx)=0
sinx=0 ⇒ [b]x=πk, k ∈ Z[/b] не входят в ОДЗ
или
3cos2x-17cosx=0
3*(2cos^2x-1)-17cosx=0
6cos^2x-17cosx-3=0
D=17^2-4*6*(-3)=289+72=361
сosx=-1/6 или сosx=3 ( уравнение не имеет корней в силу ограниченности косинуса)
cosx=-1/6
[b]x= ± arccos(-1/6)+2πn, n ∈ Z[/b]
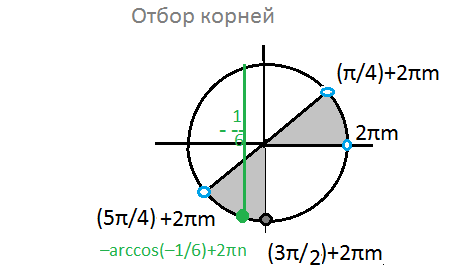
ОДЗ удовлетворяют корни:
x=-arccos(-1/6)+2πn, n ∈ Z
см. рис. 4.
О т в е т. [b] х=-(π- arccos(1/6))+2πn, n ∈ Z[/b]